MDQにおけるPainを主要アウトカムにした試験設計の考え方

- アウトライン
-
- 作成日: 2026/1/13
- 更新日: –
はじめに
Menstrual Distress Questionnaire (MDQ) は、月経関連症状を評価する尺度として広く用いられています。
サブスケールとして、
- Pain
- Water Retention
- Autonomic Reactions
- Negative Affect
- Impaired Concentration
- Behavior Change
- Arousal
- Control
で構成される多次元尺度です。
一方で、ヒト臨床試験 (ヒト試験) においてMDQをどのように用いるかについては、評価項目の選択、対象集団の定義、解析方法など、実務上の判断が求められる場面が多いです。
本稿では、MDQのPainを主要アウトカムとした場合、機能性表示食品として一般化可能性の高い試験を設計するための考え方を整理します。
今回、Painを選択した理由
MDQは、月経関連症状を月経前 (Premenstrual)・月経期 (Menstrual)・月経間期 (Intermenstrual) という3つの時期に分けて評価する点に特徴があります。
それぞれの時期は、以下のような役割を持っています。
-
月経前 (Premenstrual)
月経開始前に出現・増悪する症状を捉える時期であり、いわゆるPMSに関連する症状が反映されやすい。一方で、症状の出現様式や強さには個人差が大きく、ばらつきが大きくなりやすい。
-
月経期 (Menstrual)
月経痛や下腹部痛、腰痛など、痛みに関連する症状が最も強く現れやすい時期である。試験参加者自身も変化を最も実感しやすく、臨床的な解釈が比較的明確である。
-
月経間期 (Intermenstrual)
症状が最も軽減し、日常状態に近い時期である。個人内のベースラインとしての意味を持つ一方で、Painに関しては床効果が強く、主要評価項目としては変化を捉えにくい。
MDQ を用いたヒト臨床試験 (ヒト試験) においては、これら3時期すべてを測定することで、症状の時間的推移や個人内変動を把握することが可能になります。
そのため、ヒト臨床試験 (ヒト試験) を実施する際は、3時期すべての測定自体は実施することが望ましいと考えられます。
一方で、主要評価項目としてどの時期・どのサブスケールを用いるかについては、別途慎重な判断が必要です。
MDQには複数のサブスケールが存在しますが、本稿ではPainサブスケールを主要アウトカム (主要評価項目) として位置づけました。その理由は以下のとおりです。
- 症状概念が単一で解釈が明確
- 月経関連症状の中で臨床的に最も重要
- 試験参加者にとっても変化を実感しやすい
さらに、評価時期としては、月経期 (Menstrual) のPainに着目することが最も合理的と考えました。月経期 (Menstrual) のPainは、症状の強度が最大となりやすく、介入による改善を捉えやすい一方で、月経前 (Premenstrual) に比べてばらつきが過度に大きくなりにくく、月経間期 (Intermenstrual) に比べて床効果の影響を受けにくいという特徴があります。
このような理由から、
-
主要評価項目
▷ 月経期 (Menstrual) におけるMDQ Painサブスケールの合計得点
-
副次的または探索的評価項目
- 月経前 (Premenstrual) および月経間期 (Intermenstrual) のPain
- その他のMDQサブスケール
という位置づけが、方法論的にも実務的にも最もバランスの取れた設計であると判断しました。
(機能性表示食品として、Painが適切という意味ではないので、ご了承ください。)
複数のサブスケールや複数の時期を同時に主要アウトカムとして設定すると、多重性の問題や結果解釈の複雑化を招きやすくなります。そのため、主要は明確に1つに絞り、その他は副次的・探索的に評価するという整理は、ヒト試験において現実的かつ合理的な選択肢といえるでしょう。場合によっては、特定の副次的アウトカムを「重要な副次評価項目」として位置づけることも考えられますが、その際には多重性への配慮が不可欠です。
機能性表示食品向けの対象集団を定義する
機能性表示食品のヒト臨床試験 (ヒト試験) を計画する場合は、原則として健常者 (軽症域や境界域を含む) である必要があります。
しかし、MDQのサブスケールには軽症、中等症、重症のような基準 (カットオフ値) は設けられていません。そのため、健常者 (軽症域や境界域を含む) の選抜基準を決定するのは非常に困難です。
今回は、MDQの回答の意義をヒントに対象者を定義していきたいと思います。
これが皆様の研究のヒントになれば幸いです。
MDQの各質問項目は以下の5段階で評価されます。
- 0: No experience of symptom (症状なし)
- 1: Present, mild (軽度)
- 2: Present, moderate (中等度)
- 3: Present, strong (強い)
- 4: Present, severe (重度)
Painは6つの質問項目の合計得点であり、範囲は0–24点です。
各質問項目の回答が、0で「症状なし」、1で「軽度」であることを利用して対象者を定義してみます。
Painの合計得点とその平均得点をまとめると以下の通りです。
| 合計得点 | 平均得点 | 解釈 |
|---|---|---|
| 0~2 | 0.00~0.33 | 無症状と考えられる |
| 3~11 | 0.50~1.83 | 軽度と考えられる |
| 12~ | 2.00~ | 中等度と考えられる |
合計0–2点は、ほぼ無症状に近く、介入による改善余地がほとんどなさそうです。
このような試験参加者を含めると、floor effectにより群間差が検出されにくくなります。
合計3点は、
- 複数項目で軽度の症状が存在する
- 「症状あり」と言える最小レベル
であり、改善余地を確保する下限として合理的だと思います。
合計6点の平均得点が1.00点なので、6点を下限にすることも考えられました。
しかし、合計6点以上は、症状が明確な試験参加者層を抽出できる一方で、軽度症状者の一部を除外することとなり、結果の一般化可能性が限定されるおそれがあります。そのため今回は、floor effectを回避しつつ一般女性集団への外挿性を確保する目的で、下限を3点としました。
合計12点以上は、項目平均で2.00点に相当し、複数項目で中等度以上の症状が持続している状態です。これは軽症を超え、中等症に入り始める水準と考えられます。
よって、Painの境界域は3点以上11点以下が妥当であり、十分な一般化可能性があると考えられます。
<留意事項>
MDQにおいて、月経間期から月経前期あるいは月経期にかけて症状が30%以上変動する場合、一過性の月経関連症状を超える可能性があるため、選抜条件を設定する際は考慮したほうが良いと思います。
サンプルサイズを計算する
4.1 標準偏差 (ばらつき) を予測する
Painの合計得点が3–11点に限定した場合、標準偏差 (SD) はどの程度になるかをシミュレーションしてみましょう。
<仮定1: 3–11点が等確率で出現する場合 (一様分布)>
まず、合計得点3–11の各値がすべて同じ確率で出現すると仮定してみましょう。
これは、症状の強さに特定の偏りがなく、端の値 (3や11) にも中間値 (6や7) と同程度の試験参加者が存在する状況に相当します。
set.seed(123)
n <- 100000
# 一様分布
x_uniform <- sample(3:11, n, replace = TRUE)
sd(x_uniform)結果をみると・・・
> sd(x_uniform)
[1] 2.582829この場合、標準偏差 (SD) は約2.6点でした。
この仮定を採用する場合、標準偏差 (SD) を2.5点程度と見積もることが妥当と考えられます。
<仮定2: 下限と上限のみに集中する場合 (二点分布)
次に、試験参加者が合計3点または11点のいずれかにのみ分布するという、数学的に最もばらつきが大きくなる極端な状況を考えてみます。
set.seed(123)
n <- 100000
# 二点分布
x_extreme <- c(rep(3, n/2), rep(11, n/2))
sd(x_extreme)結果をみると・・・
> sd(x_extreme)
[1] 4.00002この場合、標準偏差 (SD) は4.0です。これは、取りうる値の範囲が 3–11 点に固定されている場合の理論的な最大値です。
<仮定3: 下限寄りと上限寄りがやや多い場合 (弱いU字型分布)>
ここまでの結果から、次のことが分かります。
- 一様分布では標準偏差 (SD) は約2.6
- 下限と上限のみに集中する極端な仮定では標準偏差 (SD) は4.0
しかし、実際の軽症集団 (Pain 合計3–11点) は、これら 2つの極端なケースの中間的な分布をとると考えるのが自然です。
軽症集団の中には、
- 症状が軽微な下限寄りの被験者 (3–4 点)
- 中等症に近い上限寄りの被験者 (10–11点)
が一定数存在する一方で、中央値付近 (6–8 点) は症状の進行や改善の過程で通過しやすく、相対的に人数が少なくなる可能性があります。
このような状況を反映した分布として、下限寄りと上限寄りがやや厚く、中央が相対的に少ない「弱いU字型分布」を仮定してみます。
set.seed(123)
n <- 100000
values <- 3:11
# 弱いU字型分布
prob_raw <- c(
0.16, # 3
0.08, # 4
0.06, # 5
0.05, # 6
0.04, # 7
0.05, # 8
0.06, # 9
0.08, #10
0.16 #11
)
# 合計1.0に正規化
prob_sd3 <- prob_raw / sum(prob_raw)
# シミュレーション
x_sd3 <- sample(values, n, replace = TRUE, prob = prob_sd3)
sd(x_sd3)結果をみると・・・
> sd(x_sd3)
[1] 3.10942この仮定の下では、標準偏差 (SD) は約3.1となりました。
なので、丸めて3.0がこの仮定の標準偏差 (SD) として問題なさそうです。
この弱いU字型分布は、
- 一様分布よりもばらつきが大きい
- しかし、下限と上限のみに集中する非現実的な最悪ケース (二点分布) ほど極端ではない
という位置づけになります。
すなわち、標準偏差 (SD) = 3.0は、現実的な分布を踏まえつつ、やや悲観的に見積もった保守的な仮定であり、恣意的に選んだ値ではなく、分布仮定から自然に導かれた値と解釈できますね。
これらの標準偏差 (SD) を利用して、サンプルサイズを計算していきましょう。
4.2 サンプルサイズの計算
ヒト臨床試験 (ヒト試験) における例数設計では、「どの程度の差を検出したいのか (群間差)」と「アウトカムのばらつきをどの程度と見込むのか (標準偏差)」が、必要な症例数 (サンプルサイズ) をほぼ決定づけます。
Painの合計得点を主要評価項目とする場合も、この点は例外ではありません。
今回は、Rのpwrパッケージを用いて、標準偏差 (SD) と群間差の組み合わせが、例数にどのような影響を与えるかを整理します。
<前提条件>
例数計算は以下の条件を仮定します。
- 2群比較
- 両側検定
- 有意水準: 0.05
- 検出力: 90%
- 群間差: 1.0~3.0 (0.5刻み)
- 標準偏差: 2.5、3.0、4.0 (前述で仮定した値)
<Rコード>
library(pwr)
library(dplyr)
# 設定
sd_vec <- c(2.5, 3.0, 4.0)
delta_vec <- seq(1.0, 3.0, by = 0.5)
alpha <- 0.05
power <- 0.90
# 計算
res <- expand.grid(
SD = sd_vec,
Delta = delta_vec
) %>%
mutate(
effect_size = Delta / SD,
n_per_group = ceiling(
mapply(
function(d) {
pwr.t.test(
d = d,
sig.level = alpha,
power = power,
type = "two.sample",
alternative = "two.sided"
)$n
},
effect_size
)
)
)
resこのコードでポイントごとのサンプルサイズが計算されますが、視覚的にわかりやすくしていきましょう。
library(ggplot2)
ggplot(res, aes(x = Delta, y = n_per_group, color = factor(SD))) +
geom_line(linewidth = 1.2) +
geom_point(size = 2) +
scale_color_manual(
values = c("steelblue", "darkorange", "darkgreen"),
name = "SD"
) +
labs(
x = "群間差 (目標差)",
y = "サンプルサイズ(1群あたりのサンプルサイズ)",
title = "サンプルサイズシミュレーション"
) +
theme_minimal(base_size = 13)出力された図がこちらです。
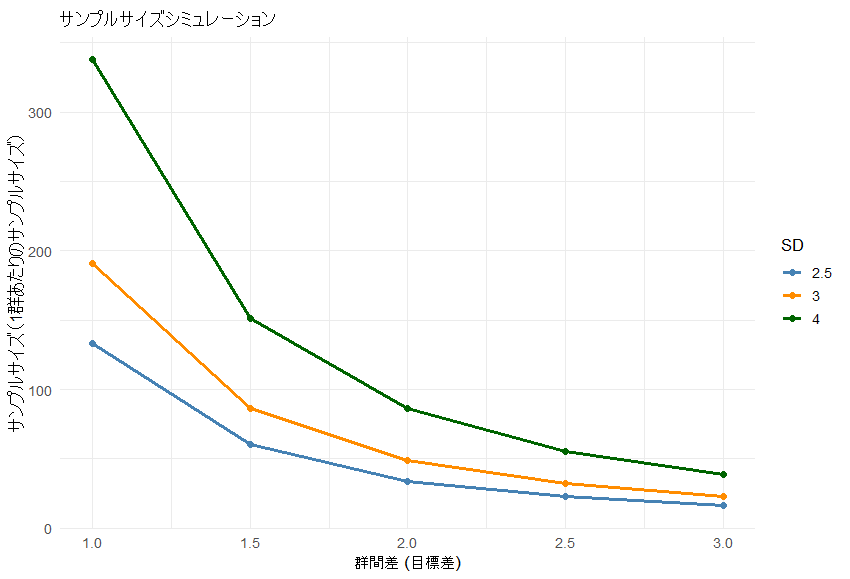
わかりやすくなりましたね。この図から、いくつか重要なポイントが読み取れます。
まず、標準偏差 (SD) が大きくなるほど、必要なサンプルサイズは急激に増加します。これは直感的にも理解しやすく、アウトカムのばらつきが大きいほど、同じ群間差を検出するためには多くの試験参加者が必要になることを意味します。
次に、検出したい群間差が小さい領域 (群間差 = 1.0〜1.5点) では、標準偏差 (SD) の仮定がサンプルサイズに与える影響が特に大きいことが分かります。たとえば、群間差 = 1.0点の場合、標準偏差 (SD) = 2.5と標準偏差 (SD) = 4.0では、1群あたりの必要例数に大きな差が生じます。このことは、「群間差をどこに置くか」と同時に、「標準偏差 (SD) をどの程度と仮定するか」が、例数設計において極めて重要であることを示しています。
一方で、群間差が2.0点以上になると、標準偏差 (SD) の違いによる影響は相対的に小さくなり、設計は安定します。この領域では、多少標準偏差 (SD) の見積もりがずれていたとしても、サンプルサイズが極端に変動することはなく、実務的に扱いやすい設計となります。
<群間差と臨床的意義の関係をどう考えるか>
ここで改めて、MDQ Pain における群間差の臨床的な意味を整理しておきます。
-
群間差 = 1.0 点
数値上は、Painの1項目が1段階改善した場合と同程度のスコア差に相当します。しかし、6項目の合計得点で1.0点の差は、複数項目での小さな変化の積み重ねなのか、1項目のみの変化なのかが判別できず、試験参加者にとって体感できる改善レベルに達しているかは不明瞭です。加えてサンプルサイズも大きくなるため、検証的試験の目標値としては設定しにくいと考えられます。
-
群間差 = 1.5 点
複数項目で軽度の改善が重なった状態に相当し、試験参加者にとっても「痛みが和らいだ」と説明しやすそうです。臨床的意義と実務性のバランスが取れた、境界域集団 (ベースラインが3-11点の集団) における現実的な下限だと思います。
-
群間差 ≥ 2.0 点
Painの複数側面で明確な改善が生じていると解釈でき、臨床的にも統計的にも安定した設計が可能です。そのため探索的試験では、最も説明しやすい改善幅だと思います。
<本稿における設計上の判断>
以上を踏まえると、MDQにおけるPainの合計得点を主要評価項目とする機能性表示食品のヒト臨床試験 (ヒト試験) においては、
- 標準偏差 (SD): 3.0 (現実的かつやや保守的な仮定)
- 主要な検出目標 (群間差): 1.5点 (検証的試験)、2.0点 (探索的試験)
を設定することが、一般化可能性・臨床的意義・試験規模のバランスという観点から、妥当な選択肢であると考えられます。
| 分類 | 探索的試験 | 検証的試験 |
|---|---|---|
| 標準偏差 (SD) | 3.0 | 3.0 |
| 群間差 (目標差) | 2.0 | 1.5 |
| 1群あたりのサンプルサイズ | 50例 | 90例 |
まとめ
MDQ Pain を主要アウトカムとして用いる場合、サンプルサイズ計算 (例数設計) は単なる計算問題ではなく、
- 対象集団をどう定義するか
- どの程度の改善を「意味のある変化」と捉えるか
- その変化を、どの程度の確実性で検出したいか
という一連の判断の積み重ねです。
また、サンプルサイズ計算によって得られる目標症例数は、「必ず有意差を出すための人数」ではなく、想定した大きさの介入効果が本当に存在するかどうかを、統計学的に十分な確実性をもって判断できる人数を意味します。
標準偏差 (SD) と群間差を系統的に動かしながら検討することで、「なぜこのサンプルサイズなのか」を説明できる設計に近づきます。本稿の考え方が、MDQを用いた試験設計を検討する際の一助となれば幸いです。
参考文献
- Moos, RH. (2010). Menstrual Distress Questionnaire (MDQ): Manual, instrument, and scoring guide (4th ed.). Mind Garden, Inc. (Original work published 1968; revised editions 1991, 2000)

