Rで糖尿病リスクを予測する

アウトライン

はじめに

医学研究において「ある要因が疾患の発症に関係しているか」を評価する場面は多く存在します。たとえば「肥満は糖尿病のリスクを高めるのか？」といった問いに答えるには、疾患の有無という二値の結果を、複数の要因から統計的に予測する手法が求められます。

ロジスティック回帰モデルは、このような疾患の発症リスクや治療効果の有無を評価するために広く使われる解析手法の一つです。

今回は、ロジスティック回帰モデルを用いて疾患の有無 (0/1) を予測し、医学論文で使われる解析の流れ・結果の読み方を実践的に解説します。

解析データセットの準備

2.1 使用する解析データセット

解析データセットは、Pima Indians Diabetes Databaseを利用します。Pima Indians Diabetes Databaseは、アメリカ国立糖尿病・消化器・腎疾患研究 (National Institute of Diabetes and Digestive and Kidney Diseases; NIDDK) によって作成されたもので、診断値に基づいて糖尿病の有無を予測することを目的としています。対象は、特定の条件のもとで抽出された21歳以上のピマ族 (Pima Indian) 女性に限定されています。

2.2 解析データセットのダウンロード

mlbenchをインストールして、データセットを取得します。

# 必要なパッケージのインストールと読み込み
install.packages("mlbench")
library(mlbench)

# データの読み込み
data("PimaIndiansDiabetes")
df <- PimaIndiansDiabetes

# 目的変数 (diabetes) を0/1に変換
df$diabetes_bin <- ifelse(df$diabetes == "pos", 1, 0)

2.3 構成を確認する

解析データセットの中身の確認と新しく生成した変数「diabetes_bin」があることを確認してみましょう。

> str(df)
'data.frame':	768 obs. of  9 variables:
$ pregnant: num  6 1 8 1 0 5 3 10 2 8 ...
$ glucose : num  148 85 183 89 137 116 78 115 197 125 ...
$ pressure: num  72 66 64 66 40 74 50 0 70 96 ...
$ triceps : num  35 29 0 23 35 0 32 0 45 0 ...
$ insulin : num  0 0 0 94 168 0 88 0 543 0 ...
$ mass    : num  33.6 26.6 23.3 28.1 43.1 25.6 31 35.3 30.5 0 ...
$ pedigree: num  0.627 0.351 0.672 0.167 2.288 ...
$ age     : num  50 31 32 21 33 30 26 29 53 54 ...
$ diabetes: Factor w/ 2 levels "neg","pos": 2 1 2 1 2 1 2 1 2 2 ...
$ diabetes_bin: num  1 0 1 0 1 0 1 0 1 1 ...

「diabetes」の情報を利用して「diabetes_bin」として二値化できました。
各変数の概要は「help(PimaIndiansDiabetes)」で確認できます。

pregnant	Number of times pregnant
glucose	Plasma glucose concentration (glucose tolerance test)
pressure	Diastolic blood pressure (mm Hg)
triceps	Triceps skin fold thickness (mm)
insulin	2-Hour serum insulin (mu U/ml)
mass	Body mass index
pedigree	Diabetes pedigree function
age	Age (years)
diabetes	Class variable (test for diabetes)

このデータセットで実際にモデルを構築していきましょう。

ロジスティック回帰モデルの構築

3.1 モデルの基本式と解釈

ロジスティック回帰モデルは、以下の式で表現できます:

\[ \log\left(\frac{p}{1-p}\right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_k X_k \]

p	: ある事象 (例: 疾患の発症、検査陽性など) が起こる確率
p/1−p	: オッズ (odds) と呼び、事象が起こる確率と起こらない確率の比
log (p/1−p)	: オッズの対数 (logit)
β0	: 切片 (基準のオッズに対応する値)
βi	: 各変数Xiの影響の大きさ (logオッズ比)

このモデルをRで構築していきます。

3.2 実際にモデルを構築する

説明変数には、pregnant、glucose、pressure、mass、ageを入れてみます。
「family = binomial」で、ロジスティック回帰モデルであることを指定します。

# ロジスティック回帰モデルの構築
model <- glm(diabetes_bin ~ pregnant + glucose + pressure + mass + age,
             data = df,
             family = binomial)

# モデル要約
summary(model)

# オッズ比と信頼区間
exp(cbind(OR = coef(model), confint(model)))

結果の解釈

4.1 係数とP値の確認

この結果をみていきましょう。

> # モデル要約
> summary(model)

Call:
glm(formula = diabetes_bin ~ pregnant + glucose + pressure +
    mass + age, family = binomial, data = df)

Coefficients:
             Estimate Std. Error z value Pr(>|z|)
(Intercept) -7.957463   0.684278 -11.629  < 2e-16 ***
pregnant     0.118803   0.031594   3.760  0.00017 ***
glucose      0.033787   0.003401   9.935  < 2e-16 ***
pressure    -0.013514   0.005104  -2.648  0.00811 **
mass         0.090961   0.014212   6.400 1.55e-10 ***
age          0.017087   0.009172   1.863  0.06249 .
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 993.48  on 767  degrees of freedom
Residual deviance: 734.99  on 762  degrees of freedom
AIC: 746.99

Number of Fisher Scoring iterations: 5

PregnantのEstimateを見ると0.119です。これは、妊娠回数が1回増えるごとにlog (オッズ) が約0.119増加することを示します。
Estimateを指数変換してオッズ比 (OR) を確認しましょう。

> # オッズ比と信頼区間
> exp(cbind(OR = coef(model), confint(model)))
              OR          2.5 %         97.5 %
(Intercept)   0.00035004  8.730627e-05  0.001279935
Pregnant      1.12614761  1.059161e+00  1.199025216
Glucose       1.03436446  1.027670e+00  1.041479827
Pressure      0.98657715  9.766267e-01  0.996430637
Mass          1.09522613  1.065871e+00  1.127008252
Age           1.01723334  9.990305e-01  1.035698680

Pregnantのオッズ比 (OR) は、1.1261でした。よって、妊娠回数が1回増えるごとに糖尿病のオッズが約12.6%増加するということになります。

4.2 モデルの性能評価

ロジスティック回帰モデルの予測性能を評価するために、ROC曲線を描き、曲線下面積 (Area Under the Curve; AUC) を算出します。

install.packages("pROC")
library(pROC)

# ROC曲線の描画とAUC
roc_obj <- roc(df$diabetes_bin, fitted(model))
plot(roc_obj, main = "ROC Curve")
auc(roc_obj)

roc() 関数でROC曲線オブジェクトを作成し、第1引数に実際のクラスラベル (diabetes_bin: 0または1)、第2引数にモデルから得られた予測確率 (fitted(model)) を入れ、各しきい値に対する真陽性率 (感度) と偽陽性率 (1-特異度) を計算します。

描画した曲線は以下の通りです:

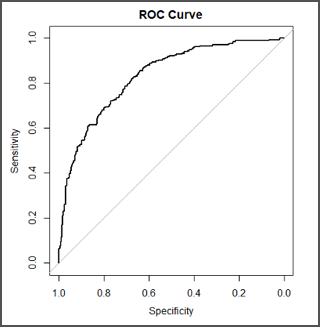
横軸: 偽陽性率 (FPR = 1 - 特異度)
縦軸: 真陽性率 (TPR = 感度)

曲線が左上に近いほど判別性能が高い。
実際にAUCの値を取得すると・・・

> auc(roc_obj)
Area under the curve: 0.8304

AUCは0.83であり、良好な識別性能を示しました。

今回のモデルは、「陽性者と陰性者の区別がつく能力が高い」ことを意味します。
つまり、「陽性の人の予測スコアが陰性の人より高くなる割合が83%」です。

論文形式での結果記載例

結果の報告例は以下の通りです:

血糖値 (OR: 1.03、95%信頼区間: 1.02–1.05、p < 0.001) およびBMI (OR: 1.09、95%信頼区間: 1.04–1.14、p < 0.001) は、糖尿病の有意な予測因子であることが示された。また、年齢もリスクのわずかな上昇と関連していました (OR: 1.02、95%信頼区間: 1.00–1.04、p=0.045)。本モデルのROC曲線下面積 (AUC) は0.83であり、良好な識別能を示した。

オッズ比 (OR) や95%信頼区間は必ず記載しましょう。

まとめ

glm() でロジスティック回帰モデル構築 → exp() でオッズ比
信頼区間は confint() で取得
ROCやAUCは pROC::roc() が便利
論文では「OR」「95%CI」「P値」「AUC」で報告