シミュレーションによるサンプルサイズ計算

- アウトライン
-
はじめに
臨床研究や介入試験を計画する際に欠かせないのが、検出力とサンプルサイズの設計です。
- 検出力とは、真に差があるときに、統計的に有意差ありと判定できる確率のことです。
- サンプルサイズは、その検出力を達成するために必要な被験者数を指します。
通常、pwrパッケージにあるpower.t.test()関数のような理論式を用いた検出力計算が主流です。しかし、実際の研究では正規分布の仮定が成り立たない場合や、分散が等しくない場合、または複雑な分布を持つ実データを使うことも多く、理論式だけでは対応しきれない場面もあります。
そこで登場するのが、モンテカルロシミュレーションです。実際のデータ構造を反映した乱数生成と繰り返し検定により、より直感的・柔軟に検出力を確認することが可能になります。
解析データセットの準備
2.1 使用する解析データセット
解析データセットは、National Health and Nutrition Examination Survey (NHANES) を利用します。NHANESは、米国疾病予防管理センター (CDC) 傘下のNational Center for Health Statistics (NCHS) によって実施されている米国の成人および子どもの健康状態に関する包括的な調査です。身体測定、健康診断、栄養調査、血液検査などを通じて、あらゆる年齢層における健康・栄養状態を把握することを目的としています。特に、栄養摂取に関する面接調査や血液検査によって、食事やサプリメントから摂取される栄養素の量が評価され、医療現場での診療のあり方や公衆衛生政策の改善にも活用されています。NHANESは、臨床データと栄養データを組み合わせた、唯一の全国規模の健康調査データベースです。
2.2 解析データセットのダウンロードと前処理
今回は、男性の収縮期血圧と女性の収縮期血圧で有意差を検出できるサンプルサイズを検証していきたいと思います。データセットは、NHANESパッケージから取得できます。
# 必要なパッケージのインストールと読み込み
install.packages("NHANES")
library(NHANES)
# データの読み込み
data(NHANES)
df <- PimaIndiansDiabetes
# 前処理: 男女+収縮期血圧ありのデータに限定
df <- NHANES %>%
filter(Gender %in% c("male", "female")) %>%
filter(!is.na(BPSysAve))
str(df)
summary(df)
# 男女別の平均・標準偏差を算出
param <- df %>%
group_by(Gender) %>%
summarise(
mean = mean(BPSysAve),
sd = sd(BPSysAve),
.groups = "drop"
)
# 各パラメータ取得
n_male <- sum(df$Gender == "male")
n_female <- sum(df$Gender == "female")
mu_male <- param$mean[param$Gender == "male"]
mu_female <- param$mean[param$Gender == "female"]
sd_male <- param$sd[param$Gender == "male"]
sd_female <- param$sd[param$Gender == "female"]
# 効果量 d を算出 (Cohen's d)
sd_pooled <- sqrt(
((n_male - 1) * sd_male^2 + (n_female - 1) * sd_female^2) /
(n_male + n_female - 2)
)
d <- as.numeric((mu_male - mu_female) / sd_pooled)
cat("効果量 d =", round(d, 3), "\n")2.3 各パラメータの結果
ここで各パラメータを見ていきましょう。
| n | mean | sd | d | |
|---|---|---|---|---|
| male | 4252 | 120.024 | 16.44721 | 0.2167882 |
| female | 4299 | 116.3064 | 17.81539 |
標準化効果量は、0.217であり比較的小さめでした。
今回は、この男性と女性の差で有意差を得るために必要なサンプルサイズを検証します。
実際は、特定の介入の有無で検証すると思います。
シミュレーション関数を設計する
次に、モンテカルロ法で検出力を求める関数を作成します。
基本的な手順は以下のとおりです:
- ① 各群から指定サンプルサイズ (例: 200人) ぶんの乱数を正規分布に基づき生成
- ② t検定を実行し、p < 0.05 かつ mean_male> mean_female のとき「検出できた」と判定
- ③ 上記を1万回繰り返して、検出できた割合を検出力とする
# シミュレーション関数
mypower_nhanes <- function(nsim = 10000, n_per_group = 200) {
count <- 0
for (i in 1:nsim) {
MYDATA <- data.frame(
GROUP = rep(c("male", "female"), each = n_per_group),
BP = c(
rnorm(n_per_group, mean = mu_male, sd = sd_male),
rnorm(n_per_group, mean = mu_female, sd = sd_female)
)
)
result <- t.test(BP ~ GROUP, var.equal = TRUE, data = MYDATA)
means <- tapply(MYDATA$BP, MYDATA$GROUP, mean)
if (means["male"] > means["female"] && result$p.value < 0.05) {
count <- count + 1
}
}
return(count / nsim)シミュレーションを利用した場合と理論式を利用した場合の比較
シミュレーションの設計ができたので、実際に検出力を計算してみましょう。また、理論式を利用した場合も計算して、どれくらい剥離しているか確認してみます。
# シミュレーションを利用した検出力計算
set.seed(123)
power_sim <- mypower_nhanes(nsim = 10000, n_per_group = 200)
cat("シミュレーションによる検出力 =", round(power_sim, 3), "\n")
# pwrパッケージで理論検出力を算出
library(pwr)
power_theory <- pwr.t.test(d = d, n = 200, sig.level = 0.05,
type = "two.sample", alternative = "two.sided")$power
cat("pwrパッケージによる検出力 =", round(power_theory, 3), "\n")結果を見ると・・・
> power_sim <- mypower_nhanes(nsim = 10000, n_per_group = 200)
> cat("シミュレーションによる検出力 =", round(power_sim, 3), "\n")
シミュレーションによる検出力 = 0.585
> power_theory <- pwr.t.test(d = d, n = 200, sig.level = 0.05,
+ type = "two.sample", alternative = "two.sided")$power
> cat("pwrパッケージによる検出力 =", round(power_theory, 3), "\n")
pwrパッケージによる検出力 = 0.58概ね同じような検出力になりましたね。
1群あたり200例だと検出力80%にはまだまだ届かなそうですね・・・
複数のサンプルサイズを代入してみましょう。
検出力が80%以上になるサンプルサイズの確認
プロットを描くと視覚的にわかkりやすいので、dplyrパッケージで描画していましょう。
# サンプルサイズごとの検出力プロット
library(dplyr)
sizes <- seq(100, 500, by = 10)
powers <- sapply(sizes, function(n) mypower_nhanes(nsim = 10000, n_per_group = n))
# プロット
plot(sizes, powers, type = "b", pch = 19,
xlab = "各群のサンプルサイズ", ylab = "検出力 (1 - β)",
main = "NHANESに基づく収縮期血圧の検出力",
xaxt = "n", yaxt = "n", ylim = c(0, 1))
# X軸:20刻み
axis(side = 1, at = seq(100, 500, by = 20))
# Y軸:0.1刻み
axis(side = 2, at = seq(0, 1, by = 0.1))
# 検出力80%の基準線
abline(h = 0.8, col = "red", lty = 2)80%で赤線を引いてさらに見やすくしていきます。
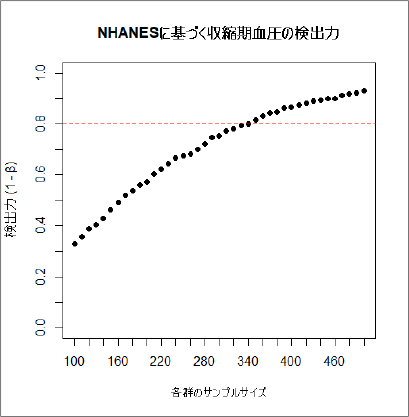
80%を超えるサンプルサイズは・・・
> sizes[which(powers > 0.8)[1]]
[1] 3401群あたり340例以上で男女間の有意差を検出できる可能性が高そうですね。
まとめ
- モンテカルロシミュレーションは、理論式が信頼できない場面でも検出力を推定可能
- 実データに近い分布を使えるため、非正規分布や複雑な構造のデータにも応用しやすい
- サンプルサイズ設計時には、理論式とシミュレーションを両方活用するのが実務的
ヒト臨床試験は、想定通りのデータを得ることができずなかなかパイロット試験を活かすことができていない事例もあります。サンプルサイズ計算にシミュレーションの考え方を導入して、試験計画を最適化していきましょう。
