機能性表示食品とクロスオーバー比較デザイン

- アウトライン
-
- 作成日: 2025/11/17
- 更新日: –
はじめに
平成27年3月30日に制定された「機能性表示食品の届出等に関するガイドライン」により始まった機能性表示食品は、令和2年4月1日の6度目のガイドライン改正 [1] をうけて、さらなる市場拡大が期待されています。最終製品を用いたヒト臨床試験 (以下、ヒト試験) による届出だけではなく、機能性関与成分のヒト試験を実施して、その結果を研究レビューに用いる事例もあり、ヒト試験の実施も活性化してきました。直近のガイドライン改正では、最終製品を用いたヒト試験の枠組みは大きな変更もなく、原則として特定保健用食品と同等の試験デザインが採用されています (表1) [1]。
表1. 機能性表示食品の届出等に関する手引き [1]
|
■(V) 様式第五号 (機能性に係る事項), 第1 様式 (V), (2) 「■科学的根拠」について各欄に必要な情報を次に掲げるとおり記載すること。, ③最終製品を用いた臨床試験(ヒト試験)により機能性を評価している場合は、「【最終製品を用いた臨床試験(ヒト試験)】」の「最終製品を用いた臨床試験(ヒト試験)により、機能性を評価している。」のボックスにチェックを付すこと。なお、本評価に当たっては、次に掲げる方法に従うこと |
|---|
|
臨床試験 (ヒト試験) の実施方法 (参加者の設定に係る考え方は除く。) は原則として、「特定保健用食品の表示許可等について」の別添2「特定保健用食品申請に係る申請書作成上の留意事項」に示された特定保健用食品の試験方法 (規格基準型、疾病リスク低減表示及び条件付き特定保健用食品に係る試験方法を除く。) に準拠することとする (同留意事項の発出前の時点において研究計画について倫理審査委員会の承認を受けた臨床試験 (ヒト試験) については、特定保健用食品に係る従前の通知に準拠していればよいこととする。)。ただし、特定保健用食品で求められる後観察期間の設定については、これを省略できるものとする。また、上記通知に示された特定保健用食品の試験方法に拠らなくても機能性の実証が可能な場合については、科学的合理性が担保された別の試験方法を用いることができる。 |
機能性表示食品の届出等に関する手引き (2025年11月18日付け消食表第543号) より引用
つまり、機能性表示食品の制度下においては、並行群間比較デザインとクロスオーバー比較デザインの2つが推奨されています (表2) [2]。中でも「食後の血中中性脂肪の上昇関係」や「食後の血糖上昇関係」、「食後の血清尿酸値の上昇関係」に関連した表示を目指す場合は、クロスオーバー比較デザインが推奨されています。しかし、「特定保健用食品の表示許可等について」や「機能性表示食品の届出等に関するガイドライン」ではクロスオーバー比較デザインにおける統計学的な留意事項は詳細に定められておらず、表2の下線部や保健の用途ごとの試験の留意事項として「作用機序等からみて十分なウォッシュアウト期間をとり、キャリーオーバー効果がないこと。」といった説明があるのみで、考慮すべき点や注意すべき点などが明示されておりません。そこで、我々は不明瞭な点を明らかにすることを課題とし、最終製品を用いたヒト試験におけるクロスオーバー比較デザインの統計学的留意事項を本稿にまとめました。
表2. 特定保健用食品の表示許可等について [2]
| ■別添2 特定保健用食品申請に係る申請書作成上の留意事項, 第2 審査申請書の留意事項, 2 審査申請書の添付資料, (4) 食品及び特定の保健の目的に資する栄養成分に係る保健の用途及び一日当たりの摂取目安量を医学的及び栄養学的に明らかにした資料, イ ヒトを対象とした試験, (イ) 試験実施上の留意点 |
|---|
| ヒト試験は、ヘルシンキ宣言の精神に則り、常に被験者の人権保護に配慮し、倫理審査委員会の承認を得て、医師の管理の下に実施する。実施に当たっては、倫理指針に従う。また、被験者の割付方法等に十分配慮し、統計学的に十分な有意差の有無を確認するに足りる試験方法と被験者を設定することが必要である。クロスオーバー試験では、試験期間が長くなることから、指標が摂取終了後に摂取前の値に回復するか (ウォッシュアウトが十分になされるか) という点に留意する必要がある。また、並行群間試験では、個人差のばらつきを解消するために、十分な例数が必要になる。なお、試験は原則として、社外ボランティアを被験者として第三者機関で実施すること。 |
特定保健用食品の表示許可等について (2025年4月23日付け消食表第357号) より引用
クロスオーバー比較デザインとは?
「機能性表示食品の届出等に関するガイドライン」におけるクロスオーバー比較デザインの統計学的留意事項をまとめるために、まずデザインの基本的な枠組みや介入効果の推定方法、クロスオーバー比較デザインの欠点を本章で解説します。
2.1 デザインの基本的な枠組み
クロスオーバー比較デザインの特徴をとらえるためにデザインの概略図を示します (図1)。クロスオーバー比較デザインは、同一の試験参加者に時期を変えて異なる介入を行うものです。並行群間比較デザインでは、異なる介入に試験参加者を割り付けますが、クロスオーバー比較デザインでは、介入の順序に対して試験参加者を割り付けます。
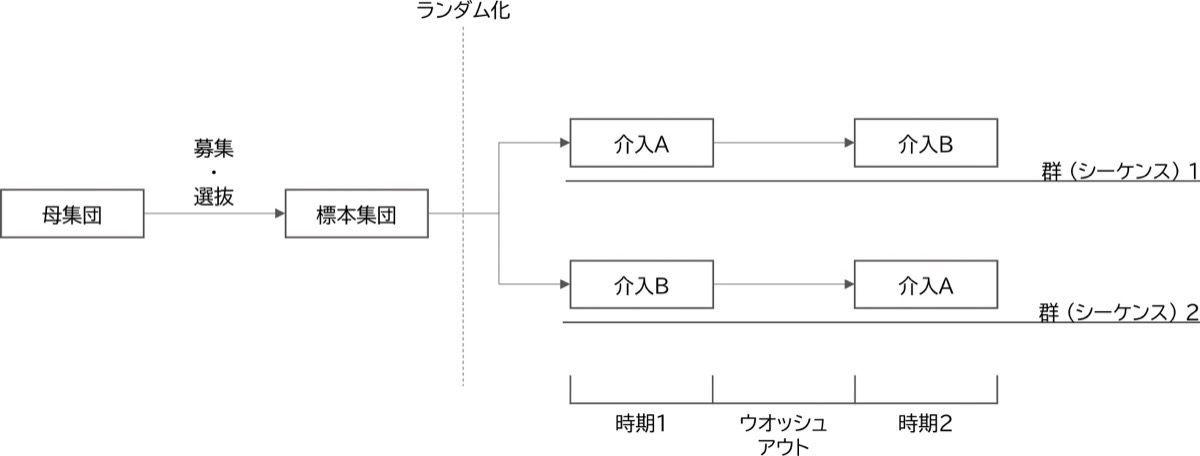
図1. 2×2×2クロスオーバー比較デザインの概略図
群 (シーケンス) 1では時期1に介入A、時期2に介入Bを施す。群 (シーケンス) 2ではその逆である。時期1の影響を取り除くために、ウォッシュアウト期間 (washout period) を設けることが多い。
図1のようなクロスオーバー比較デザインは、2剤2群2期 (2×2×2) クロスオーバー比較デザインとも呼ばれ、最も単純なデザインです。このデザインの場合はABという順序とBAという順序に試験参加者をランダムに割り付けることになります。このように2つの介入を交差させて同一の試験参加者に施すため、時期効果と呼ばれる季節変動や介入時期によって、介入の効果が異なる現象を打ち消すことができます。一方で、時期1の介入効果が残存している可能性や時期のノイズの可能性、試験期間の増大により後半 (時期2) では脱落が増える可能性があり、利点ばかりではないことに注意が必要です。
2.2 介入効果の推定
2×2×2クロスオーバー比較デザイン (図1) における介入効果を推定する方法を示します。例として、「食後の血糖上昇関係」を検証するためのヒト試験の概略を表3に示しました。
表3. 「食後の血糖上昇関係」の検証を想定したヒト試験の概略
| 対象者 | 日本人、男女両方、20歳以上、健常者 |
|---|---|
| 介入 | サプリメントX |
| 対照 | プラセボ |
| プライマリーエンドポイント | 血中グルコースのIAUC |
| 期間 | 単回摂取 |
| デザイン | 二重盲検・ランダム化・プラセボ対照・クロスオーバー比較 |
このヒト試験で得られた血中グルコースの血中濃度上昇曲線下面積 (Incremental Area Under the Curve ; IAUC) を模擬データとして表4に示しました。
表4. 「食後の血糖上昇関係」の検証試験におけるIAUCの模擬データ
| 群 | 試験参加者 | 時期1 | 時期2 |
|---|---|---|---|
|
群1 |
No. 1 | 117.00 | 182.25 |
| No. 2 | 113.50 | 126.00 | |
| No. 3 | 63.50 | 142.75 | |
| No. 4 | 77.75 | 79.75 | |
| No. 5 | 105.38 | 135.60 | |
|
群2 |
No. 6 | 115.30 | 85.75 |
| No. 7 | 143.00 | 122.75 | |
| No. 8 | 145.75 | 102.63 | |
| No. 9 | 90.85 | 70.65 | |
| No. 10 | 77.25 | 120.60 |
表5. クロスオーバー比較デザインにおけるデータの一般化
| 群 | 試験参加者 | 時期1 | 時期2 | 計 | 平均 |
|---|---|---|---|---|---|
| γ1 | 1 | y1111 | y2211 | y・・11 | m・・11 |
| : | : | : | : | : | |
| l | y111l | y221l | y・・1l | m・・1l | |
| : | : | : | : | : | |
| n1 | y111(n1) | y221(n1) | y・・1(n1) | m・・1(n1) | |
| 小計 | T111・ | T221・ | T・・1・ | – | |
| 平均 | m111・ | m221・ | – | m・・1・ | |
| γ2 | 1 | y2121 | y1221 | y・・21 | m・・21 |
| : | : | : | : | : | |
| l | y212l | y122l | y・・2l | m・・2l | |
| : | : | : | : | : | |
| n2 | y212(n2) | y122(n2) | y・・2(n2) | m・・2(n2) | |
| 小計 | T212・ | T122・ | T・・2・ | – | |
| 平均 | m212・ | m122・ | – | m・・2・ | |
| 合計 | T・1・・ | T・2・・ | TT | – | |
| 平均 | m・1・・ | m・2・・ | – | mT | |
| 介入合計 | T1・・・ | T2・・・ | TT | – | |
| 介入平均 | m1・・・ | m2・・・ | – | mT | |
i : 薬剤 (i = 1, 2)j: 時期 (j = 1, 2)k : 順序 (k = 1, 2)l: 被験者 (l = 1, ⋯, nk)
表4のデータを一般化したものが表5であり、それぞれのデータをyijkl (i: 介入、j: 時期、k: 順序、l: 試験参加者) とすると、クロスオーバー比較デザインは以下のモデルで表すことができます。
$$\begin{array}{r} y_{ijkl} = \mu + \alpha_{i} + \beta_{j} + \gamma_{k} + \varepsilon_{(1)kl} + \varepsilon_{(2)ijkl}\#(1) \end{array}$$
ここでα、β、γはそれぞれ介入、時期、順序の効果、ε(1)、ε(2)はそれぞれ試験参加者間のばらつきと試験参加者内のばらつきです。このモデルは一般線形混合モデルと呼ばれ、クロスオーバー比較デザインにおける標準的な解析手法の1つであり、表6のような分散分析表が作成されます。
表6. クロスオーバー比較デザインの分散分析表
| 要因 | 平方和 (S) | 自由度 (φ) | 平均平方和 (分散) (V) | 分散比 (F) |
|---|---|---|---|---|
| 順序効果 | Sγ | φγ | Vγ = Sγ/φγ | Fγ = Vγ/Vε(1) |
| 試験参加者残差 | Sε(1) | φε(1) | Vε(1) = Sε(1)/φε(1) | – |
| 試験参加者 | SSub | φSub | VSub = SSub/φSub | FSub = VSub/Vε(2) |
| 時期効果 | Sβ | φβ | Vβ = Sβ/φβ | Fβ = Vβ/Vε(2) |
| 介入効果 | Sα | φα | Vα = Sα/φα | Fα = Vα/Vε(2) |
| 残差 | Sε(2) | φε(2) | Vε(2) = Sε(2)/φε(2) | – |
| 全体 | ST | φT | – | – |
本稿では、統一的理解のために式 (1) における解析のステップを紹介します。まず、試験参加者数 (N) と総データ数 (n) は以下の式で表されます。
$$\begin{array}{r} N = \ \sum_{k = 1}^{2}n_{k} = n_{1} + n_{2}\#(2) \end{array}$$
$$\begin{array}{r} n = \ \sum_{j = 1}^{2}N = 2N\#(3) \end{array}$$
分散分析表を構成する要素である平方和を算出します。平方和は、順序効果 (Sγ)、試験参加者残差 (Sε(1))、試験参加者 (SSub)、時期効果 (Sβ)、介入効果 (Sα)、残差 (Sε(2))、全体 (ST) を以下の式を用いて算出します。
$$\begin{array}{r} S_{\gamma} = \sum_{j = 1}^{2}{\sum_{k = 1}^{2}{\sum_{l = 1}^{n_{k}}\left( m_{・・k・} – m_{T} \right)^{2}}} = 2\sum_{k = 1}^{2}{n_{k}\left( m_{・・k・} – m_{T} \right)}^{2} = 2N\sum_{k = 1}^{2}\left( m_{・・k・} – m_{T} \right)^{2}\#(4) \end{array}$$
$$\begin{array}{r} S_{\varepsilon(1)} = \sum_{j = 1}^{2}{\sum_{k = 1}^{2}{\sum_{l = 1}^{n_{k}}\left( m_{・・kl} – m_{・・k・} \right)^{2}}} = 2\sum_{k = 1}^{2}{\sum_{l = 1}^{n_{k}}\left( m_{・・kl} – m_{・・k・} \right)^{2}} = S_{Sub} – S_{\gamma}\#(5) \end{array}$$
$$\begin{array}{r} S_{Sub} = \sum_{j = 1}^{2}{\sum_{k = 1}^{2}{\sum_{l = 1}^{n_{k}}\left( m_{・・kl} – m_{T} \right)^{2}}} = 2\sum_{k = 1}^{2}{\sum_{l = 1}^{n_{k}}\left( m_{・・kl} – m_{T} \right)^{2}}\#(6) \end{array}$$
$$\begin{array}{r} S_{\beta} = \sum_{j = 1}^{2}{\sum_{k = 1}^{2}{\sum_{l = 1}^{n_{k}}\left( m_{・j・・} – m_{T} \right)^{2}}} = 2\sum_{j = 1}^{2}{\sum_{k = 1}^{2}{n_{k}\left( m_{・j・・} – m_{T} \right)}^{2}} = 2N\sum_{j = 1}^{2}\left( m_{・j・・} – m_{T} \right)^{2}\#(7) \end{array}$$
$$\begin{array}{r} S_{\alpha} = \sum_{i = 1}^{2}{\sum_{k = 1}^{2}{\sum_{l = 1}^{n_{k}}\left( m_{i・・・} – m_{T} \right)^{2}}} = 2\sum_{i = 1}^{2}{\sum_{k = 1}^{2}{n_{k}\left( m_{i・・・} – m_{T} \right)}^{2}} = 2N\sum_{i = 1}^{2}\left( m_{i・・・} – m_{T} \right)^{2}\#(8) \end{array}$$
$$\begin{array}{r} S_{\varepsilon(2)} = S_{T} – S_{Sub} – S_{\beta} – S_{\alpha}\#(9) \end{array}$$
$$\begin{array}{r} S_{T} = \sum_{j = 1}^{2}{\sum_{k = 1}^{2}{\sum_{l = 1}^{n_{k}}\left( y_{ijkl} – m_{T} \right)^{2}}}\#(10) \end{array}$$
クロスオーバー比較デザインにおける自由度 (φ) も同様に、群 (φγ)、試験参加者残差 (φε(1))、試験参加者 (φSub)、時期効果 (φβ)、介入効果 (φα)、残差 (φε(2))、全体 (φT) で算出します。数式は、以下の通りです。
$$\begin{array}{r} \varphi_{\gamma} = 2 – 1 = 1\#(11) \end{array}$$
$$\begin{array}{r} \varphi_{\varepsilon(1)} = \varphi_{Sub} – \varphi_{\gamma} = N – 2\#(12) \end{array}$$
$$\begin{array}{r} \varphi_{Sub} = N – 1\#(13) \end{array}$$
$$\begin{array}{r} \varphi_{\beta} = 2 – 1 = 1\#(14) \end{array}$$
$$\begin{array}{r} \varphi_{\alpha} = 2 – 1 = 1\#(15) \end{array}$$
$$\begin{array}{r} \varphi_{\varepsilon(2)} = \ \varphi_{T} – \varphi_{Sub} – \varphi_{\beta} – \ \varphi_{\alpha} = N – 2\#(16) \end{array}$$
$$\begin{array}{r} \varphi_{T} = n – 1\#(17) \end{array}$$
最後に平均平方和と分散比を算出し、分散分析表を完成させます。平均平方和は、平方和を自由度で除した値であり、分散比は平均平方和を残差の平均平方和で除した値です。なお、群の分散比は試験参加者残差で除することに注意が必要です。分散比まで求めることができれば、あとはF確率分布にあてはめて有意確率を算出するだけです。本稿では連続変数に対して式 (1) により解析しましたが、t検定など他の解析手法もあります。折笠秀樹 (2016) の文献が解析方法や報告の仕方などがまとめられているので参考になります [3]。
ここで、算出された有意確率から結果を解釈するため、主要な因子である順序効果、時期効果、介入効果の統計学的仮説を整理します。順序効果の帰無仮説は、「H0: 2群の背景因子効果は等しく、かつ対照薬と試験薬の順序効果は等しい。」となり、時期効果の帰無仮説は、「H0: 時期1と時期2の時期効果は等しい。」、介入効果の帰無仮説は、「H0: 介入Aと介入BのIAUC平均値は等しい。」となります。
模擬データをクロスオーバー比較デザイン用の分散分析表にまとめたものを表7に示しました。介入効果の有意確率が5%を下回ったことから帰無仮説である「H0: 介入Aと介入BのIAUC平均値は等しい。」が棄却され、「H1: 介入Aと介入BのIAUC平均値は異なる。」が採択されます。
表7. 2×2×2クロスオーバー比較デザインの模擬データにおける分散分析表
| 要因 | 平方和 (S) | 自由度 (φ) | 平均平方和 (分散) (V) | 分散比 (F) | 有意確率 | |
|---|---|---|---|---|---|---|
| 順序効果 | 237.705 | 1 | 237.705 | 0.213 | 0.657 | |
| 試験参加者残差 | 8929.451 | 8 | 1116.181 | 2.005 | 1.000 | 0.172 |
| 試験参加者 | 9167.156 | 9 | 1018.573 | 1.830 | 0.204 | |
| 時期効果 | 713.415 | 1 | 713.415 | 1.282 | 0.290 | |
| 介入効果 | 3353.791 | 1 | 3353.791 | 6.024 | 0.040 | |
| 残差 | 4453.537 | 8 | 556.692 | 1.000 | ||
| 全体 | 17687.898 | 19 | ||||
2.3 クロスオーバー比較デザインの利点と欠点を考える
「2.2 介入効果の推定」にて、表4の模擬データを式 (1) のモデルで解析しました。クロスオーバー比較デザインの利点は、並行群間比較デザインの解析と比較することで見えてきます。表4を並行群間比較デザインと仮定して、一元配置モデルで解析した結果を表8に示しました。
表8. 模擬データを並行群間比較として解析した場合の分散分析表
| 要因 | 平方和 (S) | 自由度 (φ) | 平均平方和 (分散) (V) | 分散比 (F) | 有意確率 |
|---|---|---|---|---|---|
| 介入効果 | 3353.791 | 1 | 3353.791 | 4.212 | 0.055 |
| 残差 | 14334.107 | 18 | 796.339 | 1.000 | |
| 全体 | 17687.898 | 19 | 17687.898 |
表7と比較して、残差の平方和が増大していることがわかります。クロスオーバー比較デザインは、時期効果や試験参加者間のばらつきを残差から分離することで介入効果の分散比の増大に寄与しています。つまり、クロスオーバー比較デザインは時期効果等を排除して介入効果を推定できることが視覚的にわかります。
次にクロスオーバー比較デザインの利点として症例数が並行群間比較デザインよりも少なくなるとされています。クロスオーバー比較デザインの症例数 (nc) は、丹後俊郎 (2003) が提案した個人差指数 (θ2) を用いることで式 (18) のように簡便に算出できます [4]。
$$\begin{array}{r} n_{c} = \frac{1}{2\left( 1 + \frac{{\sigma_{B}}^{2}}{{\sigma_{W}}^{2}} \right)}n_{p} = \frac{1}{2\left( 1 + \theta^{2} \right)}n_{p}\#(18) \end{array}$$
式 (18) より個人差指数が1、つまり試験参加者間の分散 (σB2) と試験参加者内の分散 (σW2) が等しいときのクロスオーバー比較デザインの症例数は、並行群間比較デザインの症例数 (np) の4分の1となります。このように試験参加者間のばらつきが大きい場合にクロスオーバー比較デザインを採用する利点となります。
時期効果を排除できる点や症例数を減少させる可能性があることなどの利点をあげましたが欠点もあります。この欠点を考えるために、2×2×2クロスオーバー比較デザインの模式図を図2に示しました。
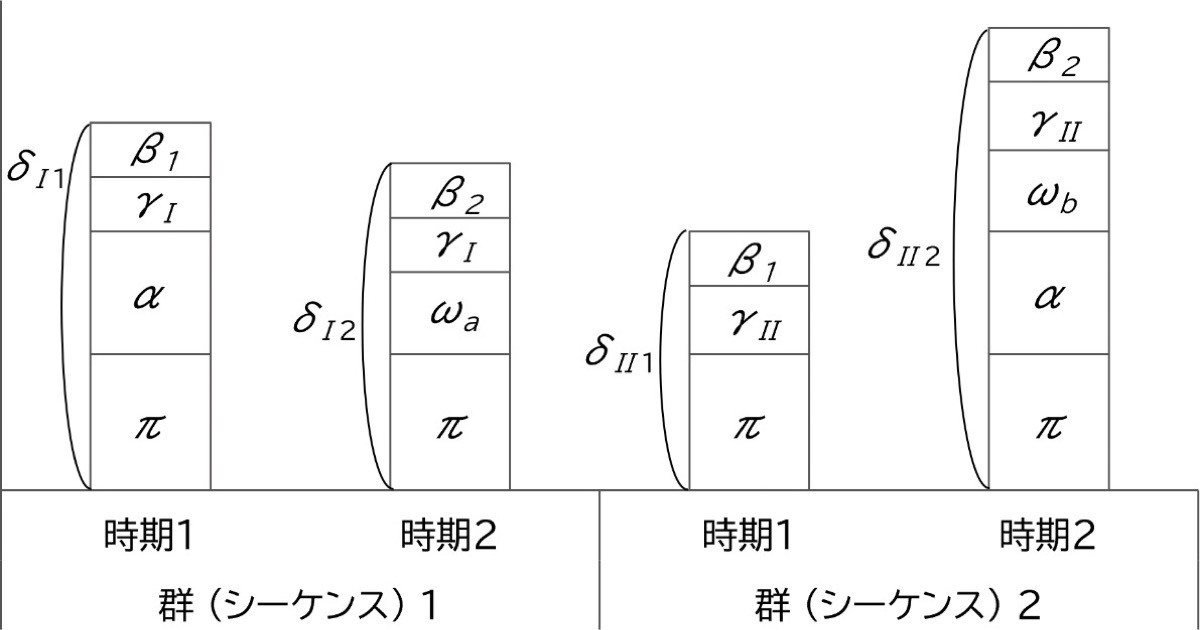
図2. 2×2×2クロスオーバー比較デザインの模式図
t1: 時期1 / t2: 時期2 / μI1: 群1の時期1 (t1) における平均値 / μI2: 群1の時期2 (t2) における平均値 / μII1: 群2の時期1 (t1) における平均値 / μII2: 群2の時期2 (t2) における平均値 / π: プラセボ効果 / α: 介入効果 / β1: 時期効果 (時期1 (t1) の効果) / β2: 時期効果 (時期2 (t2) の効果) / γI: 群1の群効果 / γII: 群2の群効果 / ωa: 介入Aの持ち越し効果 / ωb: 介入Bの持ち越し効果 / δI1 = μI1 = π + α + β1 + γI: 群1の時期1 (t1) にの平均 / δI2 = μI2 = π + ωa + β2 + γI: 群1の時期2 (t2) の平均 / δII1 = μII1 = π + β1 + γII: 群2の時期1 (t1) の平均 / δII2 = μII2 = π + α + ωb + β2 + γII: 群2の時期2 (t2) の平均
この模式図から順序効果、時期効果、介入効果がどのように計算されているのかをt検定を利用して考えます。順序効果は式 (19) のように時期1 (t1) と 時期2 (t2) の和を群間比較することで算出できます。
$$\begin{aligned} \left( \delta_{I1} + \delta_{I2} \right) – \left( \delta_{II1} + \delta_{II2} \right) & = \left( 2\pi + \alpha + \omega_{a} + 2\gamma_{I} + \beta_{1} + \beta_{2} \right) – \left( 2\pi + \alpha + \omega_{b} + {2\gamma}_{II} + \beta_{1} + \beta_{2} \right) \\ & = 2\left( \gamma_{I} – \gamma_{II} \right) + \left( \omega_{a} – \omega_{b} \right)\#(19) \end{aligned}$$
式 (19) より順序効果は群1と群2の群効果 (背景因子の差) と、介入Aと介入Bの持ち越し効果を合わせたものであり、2つの効果を分離して検出することはできません。
時期効果は式 (20) のように時期1 (t1) と 時期2 (t2) のクロス差を群間比較することで算出できます。
$$\begin{aligned} \left( \delta_{I2} – \delta_{I1} \right) – \left( \delta_{II1} – \delta_{II2} \right) & = \left( – \alpha + \omega_{a} + \beta_{2} – \beta_{1} \right) – \left( – \alpha – \omega_{b} + \beta_{1} – \beta_{2} \right) \\ & = 2\left( \beta_{2} – \beta_{1} \right) + \left( \omega_{a} + \omega_{b} \right)\#(20) \end{aligned}$$
時期効果は、式 (20) や表7のような分散分析表だけではなく、対応のあるt検定でも推定できます。群1と群2を合わせた時期1 (t1) と 時期2 (t2) の群内比較を対応のあるt検定とした場合は式 (21) となります。
$$\begin{aligned} \frac{\left( n_{1}\delta_{I2} + n_{2}\delta_{II2} \right) – \left( n_{1}\delta_{I1} + n_{2}\delta_{II1} \right)}{n_{1} + n_{2}} & = \frac{n_{1}\left( \delta_{I2} – \delta_{I1} \right) – n_{2}\left( \delta_{II1} – \delta_{II2} \right)}{n_{1} + n_{2}} \\ & = \frac{n_{1}\left( – \alpha + \omega_{a} + \beta_{2} – \beta_{1} \right) – n_{2}\left( – \alpha – \omega_{b} + \beta_{1} – \beta_{2} \right)}{n_{1} + n_{2}} \\ & = \frac{\left( n_{1} – n_{2} \right)\alpha + \left( n_{1} + n_{2} \right)\left( \beta_{2} – \beta_{1} \right) + \left( n_{1}\omega_{a} + n_{2}\omega_{b} \right)}{n_{1} + n_{2}}\#(21) \end{aligned}$$
ここで、時期効果を対応のあるt検定で推定することの問題点を考えます。群1の症例数をn1、と群2の症例数をn2としたとき、各群の症例数が等しいとき (n1 = n2 = n) は式 (22) が成り立ちます。
$$\begin{array}{r} \frac{n\left\{ \left( \delta_{I2} – \delta_{I1} \right) – \left( \delta_{II1} – \delta_{II2} \right) \right\}}{2n} = \frac{2\left( \beta_{2} – \beta_{1} \right) + \left( \omega_{a} + \omega_{b} \right)}{2}\#(22) \end{array}$$
式 (22) より、2つの群の症例数が等しい時に時期効果から介入効果 (α) を排除できます。一方で、2つの群の症例数が異なるとき (式 (21)) は、時期効果に介入効果が紛れ込んでいることがわかります。よって、式 (20) のような時期1 (t1) と 時期2 (t2) のクロス差の群間比較であれば、2つの群の症例数が異なっても時期効果から介入効果を排除できます。
介入効果は式 (23) のように時期1 (t1) と 時期2 (t2) の差を群間比較することで算出できます。
$$\begin{aligned} \left( \delta_{I1} – \delta_{I2} \right) – \left( \delta_{II1} – \delta_{II2} \right) & = \left( \alpha – \omega_{a} + \beta_{1} – \beta_{2} \right) – \left( – \alpha – \omega_{b} + \beta_{1} – \beta_{2} \right) \\ & = 2\alpha + (\omega_{b} + \omega_{a})\#(23) \end{aligned}$$
介入効果も時期効果と同様に対応のあるt検定を適用した場合を考えてみます。群1は時期1 (t1) から 時期2 (t2) を減算し、群2は時期2 (t2) から 時期1 (t1) を減算すると式 (24) となります。
$$\begin{aligned} \frac{n_{1}\left( \delta_{I1} – \delta_{I2} \right) + n_{2}\left( \delta_{II2} – \delta_{II1} \right)}{n_{1} + n_{2}} & = \frac{n_{1}\left( \delta_{I1} – \delta_{I2} \right) – n_{2}\left( \delta_{II1} – \delta_{II2} \right)}{n_{1} + n_{2}} \\ & = \frac{n_{1}\left( \alpha – \omega_{a} + \beta_{1} – \beta_{2} \right) – n_{2}\left( – \alpha – \omega_{b} + \beta_{1} – \beta_{2} \right)}{n_{1} + n_{2}} \\ & = \frac{\left( n_{1} + n_{2} \right)\alpha + \left( n_{2} – n_{1} \right)\left( \beta_{2} – \beta_{1} \right) + \left( n_{2}\omega_{b} – n_{1}\omega_{a} \right)}{n_{1} + n_{2}}\#(24) \end{aligned}$$
各群の症例数が等しいとき (n1 = n2 = n) は式 (25) が成り立ちます。
$$\begin{array}{r} \frac{n\left\{ \left( \delta_{I1} – \delta_{I2} \right) – \left( \delta_{II1} – \delta_{II2} \right) \right\}}{2n} = \frac{2\alpha + \left( \omega_{b} – \omega_{a} \right)}{2}\#(25) \end{array}$$
時期効果と同様に2つ群の症例数が等しい時に介入効果から時期効果 (β2 − β1) を取り除くことができます。症例数が異なる場合は、介入効果に時期効果が混在するため対応のあるt検定は不適切となります。そのため、式 (23) のように時期1 (t1) と 時期2 (t2) の差を群間比較するほうが適切です。
まとめると2×2×2クロスオーバー比較デザインでは持ち越し効果を数学的に排除することはできません。これは2×2×2クロスオーバー比較デザインの限界です。また、群の症例数が異なる場合は対応のあるt検定を適用してしまうと時期効果を排除することができません。また、ヒト試験では、計画時点で解析計画を固定させておくことが望ましいため対応のあるt検定を主解析とすることにはリスクを伴います。
クロスオーバー比較デザインに関する規制やガイドライン
特定保健用食品や機能性表示食品のクロスオーバー比較デザインに関する記述は、不十分であることは先述しました。本章では、クロスオーバー比較デザインに関する記載がある規制やガイドラインから課題を考えていきます。
3.1 ICH-E9 臨床試験のための統計的原則
臨床試験のための統計的原則は、日・米・EU三極医薬品規制調和国際会議 (International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use; ICH) における合意に基づき、臨床試験における統計的原則について記載したガイドラインであり、臨床試験から得られる結果の偏りを最小にし、精度を最大にすることを目標としています[5]。
このガイドラインでのクロスオーバー比較デザインの要点をまとめると
- ①二つ又はそれ以上の試験治療を行う順序をランダムに割付けられる。
- ②単純なクロスオーバー比較デザイン (2×2×2クロスオーバー比較デザイン) では、持ち越し効果が試験治療と時期間の交互作用から統計的に分離できず、どちらの効果の検定も対応する対比が「被験者間」であるため検出力に欠ける。
- ③対象とする疾患は慢性的で症状が安定しているべきである。
- ④ウォッシュアウト期間は薬剤効果が完全に消失するよう十分長くすべきである。
- ⑤最も注意すべきことは、被験者の減失に起因する解析と解釈の複雑さである。
- ⑥クロスオーバー計画は、一般に試験からの被験者の減失が少ないと期待できる場合に限定すべきである。
- ⑦2×2クロスオーバー計画が一般的に使用されており、通常その妥当性が満たされているのは、同一薬剤の異なる二つの剤型間で生物学的同等性を示す場合である。
があげられます。
これらの要点が機能性表示食品にも適用できるか考えます。
まず①と④は、「特定保健用食品の表示許可等について」にもある通り原則として二重盲検査およびランダム化を施す必要があることから適用することになります。
②、⑤、⑥は、「2.3 クロスオーバー比較デザインの利点と欠点を考える」で示した通り、クロスオーバー比較デザインの欠点です。これらは、デザインの特性上、避けることができない問題です。よって、ヒト試験を計画する際は、十分に気をつける必要があります。
③は、原則として疾病を有する者はヒト試験に組み入れることはできないので問題はないと考えられます。
最後に⑦です。クロスオーバー比較デザインは、根本的に②のような欠点を孕んでいます。しかし、後発医薬品の生物学的同等性試験ガイドラインに関する質疑応答集 (Q&A) におけるQ41の回答にある通り、「同一薬物のバイオアベイラビリティの比較試験を行う生物学的同等性試験に限っては、プロトコルが遵守されていれば、持越し効果が生じることは本来考えにくいので、持越し効果に関する考察を問わないことにした」とされています[6、7]。
機能性表示食品制度下におけるヒト臨床試験の対象者は原則として疾病を有する者の組み入れはないことや介入がサプリメント等の食品であることからも2×2×2クロスオーバー比較デザインの採用は許容されるべきと考えられますが、「機能性表示食品の届出等に関する手引き」や「特定保健用食品の表示許可等について」でも明示されていないため、今後の課題としてあげられます。
表9. ICH-E9 臨床試験のための統計的原則におけるクロスオーバー比較デザインに関する記述 [5]
| III. 試験計画上で考慮すべきこと, 3.1 試験計画の構成, 3.1.2 クロスオーバー計画 |
|---|
| クロスオーバー計画では、各被験者は二つ又はそれ以上の試験治療を行う順序をランダムに割付けられる。したがって被験者自身を対照として試験治療比較が行われることになる。この単純な計画上の工夫は、主として、それを行うことが、定められた検出力の達成に必要な被験者数と通常は評価件数を劇的に減少させることがあるという理由から魅力的である。最も単純な2×2クロスオーバー計画では、各被験者は、多くの場合ウォッシュアウト期間をはさんで連続した二つの試験治療期間に、二種の試験治療のそれぞれをランダム化された順番で受ける。この計画の最も一般的な拡張では、n (>2) 個の試験治療をn期間で各被験者がすべて受け、試験治療を比較することになる。計画の拡張には、各被験者がn (>2) 個の試験治療の一部だけを受ける、同じ試験治療を繰り返し行う、といった様々な変法が存在する。・・・(以下、省略) |
ICH-E9 臨床試験のための統計的原則より引用
表10. 「後発医薬品の生物学的同等性試験ガイドラインに関する質疑応答集 (Q&A) の持越し効果に関する記述 [7]
| Q-41 持越し効果が有意になった場合には試験をやり直さなければならないか. |
|---|
| (A) 一般的には, 2剤2期クロスオーバー法では, 群効果と持越し効果とは区別がつかない. 持越し効果が有意になった場合には結果の解釈が不能であるが, 群効果が有意の場合には結果の解釈は可能である. 従来は, 群間の割付けに偏りがあるなど, 持越し効果ではなく群効果による有意差であるという考察が行われた場合には, 結果を受け入れてきた.しかし, 通常, 割付上の偏りがあったことを証明することは困難であり, また, 同一薬物のバイオアベイラビリティの比較試験を行う生物学的同等性試験に限っては, プロトコルが遵守されていれば, 持越し効果が生じることは本来考えにくいので, 持越し効果に関する考察を問わないことにした. |
「後発医薬品の生物学的同等性試験ガイドラインに関する質疑応答集 (Q&A) より引用
3.2 CONSORT 2010 Statementの拡張ガイドライン
クロスオーバー比較デザインを採用した臨床試験の報告ガイドラインが、CONSORT 2010 Statementの拡張ガイドラインとしてDwan Kら (2019) より公表されました。
この拡張ガイドラインは、クロスオーバー比較デザインの方法論的特徴の要約、公表済みのクロスオーバー比較デザインのレビュー、クロスオーバー比較デザインのためのチェックリストの提案を目的としています [8]。学術論文を執筆する際に参考にするだけではなく、ヒト試験の計画段階からチームで共有し、解析計画をはじめとしたプロトコルの執筆にも参照すべきです。
高次デザインへの拡張
式 (19) やICH E9 [5] より、2×2×2クロスオーバー比較デザインは、持ち越し効果を分離できていないことがわかりました。しかし、「特定保健用食品の表示許可等について」において保健の用途ごとの試験の留意事項として「作用機序等からみて十分なウォッシュアウト期間をとり、キャリーオーバー効果がないこと。」といった説明がある通り持ち越し効果を分離して介入効果を推定することが望ましいです。そこで、持ち越し効果を分離することができるデザインとして2×2×2クロスオーバー比較デザインを高次なデザインへと拡張することが提案されています [9]。
本章では、例として図3に示したような2剤2群3期 (2×2×3) クロスオーバー比較デザインを紹介します。このデザインは、時期3において時期2と同様の介入を施します。そのため、2×2×2クロスオーバー比較デザインよりも試験期間が延長されるので試験参加者の脱落率は増大する可能性があります。しかし、同じ介入を続けて施すことによる持ち越し効果のデータが得られるため、持ち越し効果を解析モデルに組み込むことができます。具体的には、時期1では各群の持ち越し効果はないものとします。
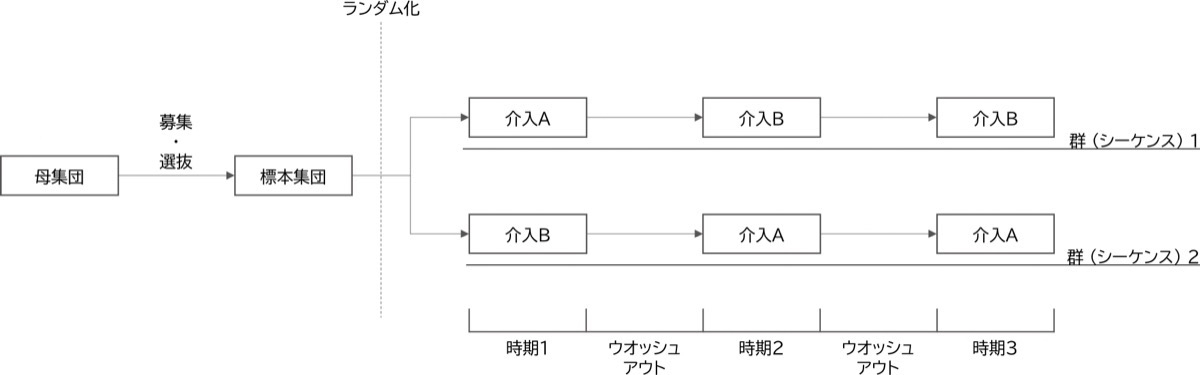
図3. 2×2×3クロスオーバー比較デザインの概略図
群 (シーケンス) 1では時期1に介入A、時期2と時期3に介入Bを施す。群 (シーケンス) 2では時期1に介入B、時期2と時期3に介入Aを施す。
時期2では群1で介入Aの持ち越し効果、群2で介入Bの持ち越し効果が発生します。時期3では群1で介入Bの持ち越し効果、群2で介入Aの持ち越し効果が発生します。これらの持ち越し効果を解析モデルに組み込みますが、時期効果をモデルに組み込むと持ち越し効果を推定できないことに注意が必要です。表11の模擬データを実際に解析した結果が表12です。この分散分析表に示す通り、群効果とは別に持ち越し効果を残差から分離させています。
表11. 「食後の血糖上昇関係」の検証試験を2×2×3クロスオーバー比較デザインで実施した場合のIAUCの模擬データ
| 群 | 試験参加者 | 時期1 | 時期2 | 時期3 |
|---|---|---|---|---|
|
群1 |
No. 1 | 125.00 | 128.00 | 101.00 |
| No. 2 | 51.25 | 59.00 | 58.50 | |
| No. 3 | 102.75 | 84.00 | 60.88 | |
| No. 4 | 65.75 | 142.75 | 59.00 | |
| No. 5 | 138.25 | 87.00 | 56.00 | |
|
群2 |
No. 6 | 154.75 | 143.00 | 99.50 |
| No. 7 | 35.31 | 28.95 | 70.00 | |
| No. 8 | 68.25 | 140.00 | 79.00 | |
| No. 9 | 77.25 | 85.75 | 122.75 | |
| No. 10 | 145.75 | 80.75 | 129.50 |
表12. 2×2×3クロスオーバー比較デザインの模擬データにおける分散分析表
| 要因 | 平方和 (S) | 自由度 (φ) | 平均平方和 (分散) (V) | 分散比 (F) | 有意確率 | |
|---|---|---|---|---|---|---|
| 群効果 | 325.189 | 1 | 325.189 | 0.145 | 0.714 | |
| 試験参加者残差 | 19745.806 | 9 | 2247.343 | 2.399 | 1.000 | 0.062 |
| 試験参加者 | 20070.995 | 10 | 2050.991 | 2.189 | 0.078 | |
| 持ち越し効果 | 1974.799 | 2 | 987.400 | 1.054 | 0.370 | |
| 介入効果 | 357.449 | 1 | 357.449 | 0.382 | 0.545 | |
| 残差 | 15927.872 | 17 | 936.934 | 1.000 | ||
| 全体 | 38331.115 | 30 | ||||
このように高次のデザインに拡張することで、持ち越し効果を排除することができます。ウォッシュアウト期間の設定根拠がない場合など介入効果が持ち越し効果の影響を受けている可能性があるヒト試験でも、持ち越し効果を排除することにより介入効果の有意差を検出しやすくすることができます。しかし、持ち越し効果が発生しないように十分なウォッシュアウト期間を設けることが重要であることに変わりありません。
まとめ
本稿は、機能性表示食品制度下におけるクロスオーバー比較デザインについて統計学的留意事項をまとめました。
時期効果を排除できることや症例数を減少させることなどのメリットが目立ちますが、試験期間の延長による脱落率の上昇や持ち越し効果の推定が困難であることが問題点としてあげられました。
特に持ち越し効果は、重要な課題です。ヒト試験の対象者が疾病者ではないことや介入がサプリメントなどの食品であり、医薬品ほどの介入効果に及ばない可能性があることから推察するとウォッシュアウト期間を適切に設けておけば、持ち越し効果が生じることは考えにくいです。
とくに食後の血中濃度関係のような単回摂取を想定しているヒト試験は、持ち越し効果が生じることは考えにくいです。しかし、「特定保健用食品の表示許可等について」にある通り、ヒト試験でクロスオーバー比較デザインを採用した場合には、持ち越し効果がないことが推奨されていることから、持ち越し効果の推定方法や結果の報告、考察の有無は、機能性表示食品制度の今後の課題です。
参考文献
- [1]消費者庁. 機能性表示食品の届出等に関する手引き (2025年10月1日付け消食表第543号) (2025年11月17日アクセス可能:
https://www.caa.go.jp/policies/policy/food_labeling/foods_with_function_claims/notice/assets/food_labeling_cms205_251001_41.pdf) - [2]消費者庁. 特定保健用食品の表示許可等について (2025年4月23日付け消食表第357号) (2025年11月17日アクセス可能:
https://www.caa.go.jp/policies/policy/food_labeling/foods_for_specified_health_uses/notice/assets/food_labeling_cms206_20250423_04.pdf) - [3]折笠秀樹. クロスオーバー試験の計画および解析. 薬理と治療. 2016; 44 (9): 1261-76.
- [4]丹後俊郎. 無作為化比較試験―デザインと統計解析 (医学統計学シリーズ). 初版、朝倉書店、2003、179-83p.
- [5]厚生労働省. ICH E9 臨床試験のための統計的原則 (2025年11月17日アクセス可能:
https://www.pmda.go.jp/files/000156112.pdf) - [6]厚生労働省. 後発医薬品の生物学的同等性試験ガイドライン (令和2年3月19日薬生薬審発0319第1号、別紙1) (2025年11月17日アクセス可能:
https://www.pmda.go.jp/files/000234565.pdf) - [7]厚生労働省. 後発医薬品の生物学的同等性試験ガイドライン質疑応答集 (Q&A) (令和2年3月19日事務連絡、別紙1) (2025年11月17日アクセス可能:
https://www.pmda.go.jp/files/000234569.pdf) - [8]Dwan K、Li T、Altman DG、Elbourne D. CONSORT 2010 statement: extension to randomised crossover trials. BMJ. 2019; 366: l4378. (PMID: 3136659)
- [9]Jones B、Kenward MG. Design and Analysis of Cross-Over Trial. 3rd edition、Chapman and Hall、2014、113-7p. (DOI:
https://doi.org/10.1201/b17537)

