機能性表示食品のためのメタアナリシス

- アウトライン
-
- 作成日: 2025/11/10
- 更新日: –
メタアナリシスを始める前に
メタアナリシスを始める前に振り返ってほしいことがあります。メタアナリシスに用いる文献は適切に集められていることが重要です。レビュー自体が何を明らかにしたいのか明確に定義されており、「どの介入を比較するのか」、「どのアウトカムを解析するのか」をあらかじめ計画されている必要があります。
注意点を以下にまとめました。
-
- メタアナリシスに飛びつく前に
- ダイヤが出る瞬間は魅力的だが、前提条件が不十分なら結果は誤解を招く。
-
- レビューの明確化
- 何を明らかにしたいのか (PICO要素) を定義しないと、解釈不能になる。
-
- 適格基準・研究選択
- 研究をどの条件で含め/除外するかを明示的に定めないと、恣意的な統合になる。
-
- データ収集とバイアス評価
- 欠測や測定法の違いを確認し、リスク・オブ・バイアスを事前に見極める。
-
- 介入比較・分析対象の設計
- どの群を比較するか、どのアウトカムを解析するかをあらかじめ計画しておく。
メタアナリシスはレビューの最終工程であることを理解し、適切な計画をたてましょう。
メタアナリシスの原則
メタアナリシスの一般的な手法は、以下の基本的な原則に従っています:
- メタアナリシスは通常、2段階のプロセスです。第1段階では、各研究に対して要約統計量が計算され、すべての研究で観察された介入効果を同じ方法で記述します。例えば、データが2値変数の場合は、要約統計量はリスク比となる場合があります。データが連続変数の場合は、要約統計量は平均値の差となります。
-
第2段階では、個々の研究で推定された介入効果の加重平均として、統合された介入効果の推定値が計算されます。
\[ \text{加重平均} = \frac{\sum_i Y_i W_i}{\sum_i W_i} \]Yi は第 i 番目の研究で推定された介入効果、Wi は第 i 番目の研究に付与された重み、そして和はすべての研究にわたるものです。
注意: すべての重みが同じ場合、加重平均は介入効果の平均値と等しくなります。第 i 番目の研究に付与される重みが大きいほど、その研究は加重平均への寄与が大きくなります。
- 複数の研究における介入効果の推定値を組み合わせる際、オプションとして、各研究が同じ介入効果を推定しているのではなく、研究間で分布に従う介入効果を推定しているという仮定を組み込むことができます。これがランダム効果メタアナリシスです。一方、各研究が正確に同じ量を推定していると仮定する場合、固定効果メタアナリシスが実施されます。
- 要約介入効果の標準誤差は、要約推定値の精度(または不確実性)を示す信頼区間を導出するために使用され、また、介入効果がないという null 仮説に対する証拠の強さを示す P 値を導出するために使用されます。
- メタアナリシスのすべての方法は、介入効果の要約定量化を提供するだけでなく、個々の研究の結果間の変動がランダムな変動と一致するかどうか、またはその変動が研究間で介入効果の不一致を示すほど大きいかどうかを評価する機能を備えています。
- 欠測データの問題は、メタアナリシスを実施する際には考慮しなければならない数多くの実践的な課題の一つです。特に、レビューの著者は、個々の参加者からのアウトカムデータの欠測 (追跡不能や解析からの除外によるもの) がもたらす影響を検討する必要があります。
メタアナリシスにおける汎用的な逆分散法 (Inverse-variance; IV) アプローチ
はじめに、メタアナリシスの代表的な統合方法である逆分散法を紹介します。逆分散法は、各研究に与えられる重みが、効果推定値の分散の逆数、すなわち、その標準誤差の二乗の逆数に設定されます。
したがって、標準誤差が小さい大規模な研究には、標準誤差が大きい小規模な研究よりも大きな重みが与えられることになります。この重みの選択は、プールされた効果推定値の不確実性を最小化します。
|
固定効果モデル (Fixed-effect) |
ランダム効果モデル (Random-effects) |
|---|---|
|
すべての研究が同じ真の効果を推定 \[ W_i = \frac{1}{SE_i^2} \] レビューに含まれる試験に限り効果を推定できる。 |
研究ごとに異なるが関連する効果を推定 \[ W_i = \frac{1}{SE_i^2 + \tau^2} \] 母集団の「平均効果」を推定するため、将来の研究にも適用可能となる。 |
この逆分散法は、固定効果モデル、ランダム効果モデルといった2つの枠組みの上でそれぞれ成立します。固定効果モデルは、すべての研究が同じ真の効果を推定するものです。つまり、大きい研究ほど統合結果に影響します。
ランダム効果モデルは、数式に示した通り、研究間分散 (τ2) を含めて重みを計算します。これは、研究ごとに「異なるが関連する効果」を推定することにつながります。そのため、小規模な研究でも統合結果に影響する可能性があります。それぞれのモデルに特徴がありますが、異質性を含めて重みを計算できるランダム効果モデルを主解析とすることが推奨されます。
2値変数を統合する場合の留意点
逆分散法の他にも統合方法があります。2値変数のメタアナリシスには、Mantel–Haenszel (マンテル・ヘンツェル) 法、Peto (ピート) 法、逆分散法が広く用いられています。Mantel–Haenszel法はイベントが稀な場合に標準誤差推定の安定性が高く、固定効果モデルにおいて一般的に推奨されます。
|
固定効果モデル (Fixed-effect) |
ランダム効果モデル (Random-effects) |
|---|---|
|
Mantel–Haenszel (MH)
Peto Odds Ratio (Peto OR)
Inverse-variance (IV) |
Inverse-variance (IV) |
一方、Peto法はオッズ比に限定されるものの、イベント発生率が1%未満かつ群サイズに大きな不均衡がない場合に最も良好な特性を示すとされます。ただし、大きな介入効果や群不均衡が存在する場合にはバイアスが生じやすく、汎用性には制限があります。逆分散法は柔軟にさまざまな効果量を扱える利点がありますが、希少イベントにおいては大標本近似に基づくため推定が不安定になります。ゼロセルを含む研究では連続性補正されることがありますが、これにより推定値が「差がない」方向に偏る可能性も指摘されています。
- ゼロセル問題
- 2×2表でイベント数=0が出るとORやRRが計算できない。
| A | B | |
|---|---|---|
| 治療群 | 0 | 100 |
| 対照群 | 2 | 98 |
↓
0.5を加える「continuity correction」を用いるとバイアスの原因になる。
↓
- イベント率 <1% (群サイズ均衡)
Peto OR が最も安定 - イベント率 >1% or 群サイズ不均衡
Mantel–Haenszel
効果量の選択については、相対効果指標が一貫性高く、一般的に推奨されます。一方、リスク差や治療必要数は解釈が簡単ですが、分散推定が不安定で稀なイベントの解析には不適とされています。総じて、イベントが希少な場合は方法論的選択が結論に大きく影響するため、複数の手法を用いた感度分析を計画しましょう。
連続変数を統合する場合の留意点
5.1 連続変数に適した効果指標 (効果量)
連続変数のメタアナリシスにおける標準的な前提は、各群でアウトカムが正規分布に従うことです。この前提は必ずしも満たされていませんが、大規模研究における影響は小さいです。しかし、アウトカムの分布が歪んでいる可能性については考慮しておく必要があります。
連続変数の主要な効果量としては平均差と標準化平均差が広く用いられています。これらはそれぞれMDとSMDのように訳すので本稿では、この言葉を使用させてください。MDは全ての研究が同一尺度で報告している場合に適しており、SMDは異なる尺度を用いる研究を統合する際に有効です。その他の効果量として「平均の比」がありますが、測定値が常にゼロより大きい場合にのみ適用可能です。
|
平均差 Mean Difference (MD) |
標準化平均差 Standardized Mean Difference (SMD) |
|
|---|---|---|
| SD の役割 |
|
|
| 意味 |
|
|
| 適切さの条件 |
|
|
MDとSMDは、それぞれ標準偏差の果たす役割が異なります。MDでは標準偏差は研究の重み付けに用いられ、標準偏差が小さい研究は大きな重みを持ちます。一方、SMDでは標準偏差はMDを標準化するために用いられ、標準偏差が小さい研究ではSMDが大きく推定されます。
このため、SMDの利用には「研究間の標準偏差の違いは測定スケールの違いのみを反映し、測定の信頼性や母集団の多様性を反映しない」という前提が必要です。
したがって、連続変数のメタアナリシスにおいては、アウトカム尺度の一貫性と研究間の標準偏差の解釈を十分に検討したうえで、効果量を選択することが不可欠です。
5.2 ベースラインからの変化量の取り扱い
連続変数を統合する際に、変化量を統合する選択肢がでてきます。
まず、変化量に基づく解析は、ベースラインからの変化量を用いることで個人間のばらつきの一部を除去でき、介入後の測定値を直接比較するより効率的かつ検出力が高くなる場合があります。
一方で、変化量は測定誤差の影響を受けやすく、特にアウトカムが不安定または測定が困難な場合には精度を損なう可能性があります。また、ベースライン値の分布が歪んでいる場合には、変化量を用いることで分布の歪みが緩和されることもあります。ベースラインの影響を適切に調整する統計的アプローチとしては、共分散分析や回帰モデルにおいてベースライン値を共変量に含める方法が推奨されています。これにより、より精密かつバイアスの少ない効果推定が可能ですが、メタアナリシスに取り込む際は汎用逆分散法を用いる必要があります。
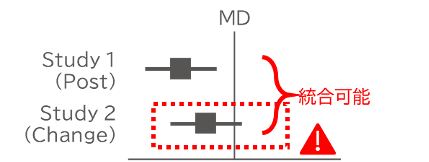
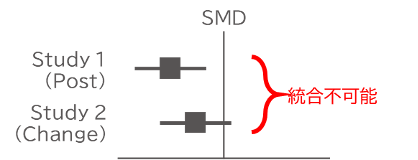
実際のレビューでは、介入後の値と変化量が混在して報告されていますが、MDを用いる限り両者を統合することに統計的な問題はありません。ただし、平均値や標準偏差の絶対値が異なるため、読者の混乱を避ける目的でサブグループとして区別することが望ましいことを覚えておいてください。
一方で、SMDを効果量とする場合は注意が必要です。SMDの標準化に用いられる標準偏差は、介入後スコアでは単一時点での個人間変動を反映するのに対し、変化量では個人内変動と個人間変動の両方を含むため、両者を直接統合することは推奨されていません。
| MD における統合 | SMD における統合 |
|---|---|
|
|
|
実証研究においては、介入後の値と変化量を用いたSMDの統合結果に差がみられなかったとする報告もありますが、実務的には介入後の値の標準偏差で標準化する方法が提案されています。
変化量の解析について (変化量の問題点)
- ベースライン値と変化量が負の相関を持つことが多い
- ベースラインの不均衡 (ランダム化の偶然による差) を十分に補正できない
- SEが過大または過小になり、検出力や信頼区間の妥当性が損なわれる
その他の変数を統合する場合の留意点
次にその他の変数として、順序尺度やカウントデータ、時間イベントがあります。
順序尺度は、原著研究の分析方法に応じて二値化または連続データとしてメタ分析されることが多いです。カテゴリ数が少なく、全研究で同じ尺度が用いられている場合には、比例オッズモデルを利用してオッズ比として統合することも可能であり、二値化より効率的にデータを活用でます。しかし、臨床的解釈が難しく、高度な統計ソフトウェアが必要です。比例オッズモデルから得られたログオッズ比と標準誤差は汎用逆分散法で統合できます。カテゴリの定義が研究ごとに異なる場合でも、適切な方法を用いることで統合可能とされています。
カウントデータは、同一被験者が複数回経験するイベントのことです。観察期間を考慮すれば率データとなり、特に稀なイベントに適しています。率比や率差として表現でき、汎用逆分散法やポアソン回帰による統合が可能です。ただし、基礎リスクが一定であるという仮定が必要であり、現実の臨床データではしばしば成立しないため解釈に注意が必要です。実際には、率比はリスク比と近似する場合がありますが、介入が「複数回のイベント発生」に影響を及ぼす場合には両者は異なる結果を示します。
時間イベントのメタ分析には主に2つの方法があります。O–E統計量と分散を用いる方法とCox (コックス) 比例ハザードモデルから得られたlog (ログ) ハザード比と標準誤差を用いる方法です。両者が混在する場合も、ログランク推定値をlogハザード比に変換することで統合できます。
| アウトカムタイプ | 研究単位の 主な解析例 |
効果指標 | 統合方法 | 注意点 留意事項 |
|---|---|---|---|---|
|
順序尺度 (Ordinal) |
|
|
|
|
|
カウント・率 (Counts & rates) |
|
|
|
|
|
時間イベント (Time-to-event) |
|
|
|
|
SMDを利用した2値変数と連続変数の統合
同じアウトカムが一部の研究では連続変数、別の研究では2値変数として報告される場合があります。2値変数は直感的に理解しやすいですが、カットオフの設定は恣意的であり、連続変数を二値化する過程で情報が失われます。このような混在に対応する方法として、以下の流れで統合します。
まず、研究者や論文からデータを集めます。次に、連続変数、2値変数、その他のように整理します。そして、連続変数やオッズ比をSMDに変換し、統合します。
小児期の不安障害に対する選択的セロトニン再取り込み阻害薬 (SSRI) の有効性を評価した5つの臨床試験の架空データを以下に示します。
| Trial | Scale | Type | SSRIs | Placebo | SMD の計算方法 | SMD | ||
|---|---|---|---|---|---|---|---|---|
| Sample size | Mean (SD) | Sample size | Mean (SD) | |||||
| 1 | Pediatric anxiety rating scale | continuous | 100 | 8 (4) | 100 | 12 (3) | MD / pooled SD | -1.13 |
| 2 | Trial 1 と同じ | continuous | 250 | 7.5 (3) | 250 | 11 (2) | MD / pooled SD | -1.37 |
| 3 | Screen for child anxiety related emotional disorders | continuous | 200 | 20 (15) | 200 | 35 (15) | MD / pooled SD | -1.00 |
| 4 | Trial 3 と同じ | continuous | 150 | 21 (11) | 150 | 31 (12) | MD / pooled SD | -0.87 |
| 5 | No scale data | binary | 300 | 150 Number who improved |
300 | 100 Number who improved |
√3 / π · lnOR | -0.38 |
5つのうち4つが連続変数で1つが2値変数です。研究1と2が同じスケールを利用していますが、3と4は別のスケールを利用しています。研究5は、医師の評価です。これらはスケールが異なりますが、似ている集団に対して小児の不安症状を調査していることが共通しています。
このようにスケールや変数の種類が異なっていても、同じ上位概念を測定しているのであれば、SMDに変換することで統合が可能です。ただし、標準偏差の違いが測定スケールの差に由来するという前提が必要であり、集団のばらつきや測定信頼性の違いを反映している場合には解釈に注意が必要です。
反復測定データを統合するためのアプローチ
ここからメタアナリシスを行うで、よくある課題の解決方法をいくつか紹介していきます。まず、反復測定データについてです。
RCTでは、6か月・1年・2年といった複数時点の結果が報告されることが多いです。しかし、同一研究内の複数時点データをそのままメタアナリシスに組み込むと、解析単位のエラーが生じるため、注意が必要です。
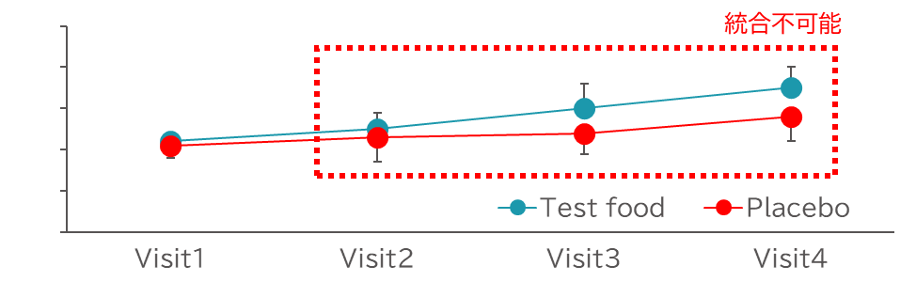
主な対応方法を4つ紹介します。
1つ目が、「個別データを用いる」ということです。これは、IPD解析と呼ばれます。すべての研究の個別データをあつめて、同一の解析モデルで解析することができるので、時点をモデルに加えたりすることができるため、解析単位のエラーはありません。
2つ目が、複数アウトカムに分けてサブグループ解析します。例えば、追跡期間を短期・中期・長期などに分類し、それぞれ独立して解析するということです。
3つ目が単一時点を選択して解析します。つまり、1つの時点に限定して解析します。臨床的に重要な時点を選ぶのが望ましいですが、利用可能なデータを最大化する観点でこの方法が採用される場合もあります。バイアスのリスクに注意が必要です。
4つ目が、最終時点を使用して解析します。各研究から最も長期のデータを採用します。ただし、研究間での一貫性が失われ、異質性が増大する可能性があることに注意してください。
このような手法を用いて、解析単位のエラーが生じないように計画をたてていきましょう。

3群以上のデータを統合するためのアプローチ (1)
次に3群以上のデータがある場合です。
以下に、3群RCTにおける連続変数データをのせます。
| Dietary intervention (face-to-face) |
Dietary intervention (online) |
No intervention | ||||
|---|---|---|---|---|---|---|
| outcome | Sample size | Mean (SD) | Sample size | Mean (SD) | Sample size | Mean (SD) |
| BMI | 49 | 35.2 (7.5) | 47 | 34.8 (8.2) | 52 | 37.1 (7.6) |
Axon E, et al (2023) のtable4より引用、改変
対面の栄養指導、オンラインの栄養指導、介入なしとしての対照群の3つの介入をした場合のBMIです。
このまま統合すると、対照群がダブルカウントされ解析単位にエラーが生じます。
そこで、これらに対応するための方法を3つ紹介します。
9.1 アプローチ1: 介入を統合する
1つ目のアプローチが介入を統合するということです。ここでは、対面の栄養指導とオンラインの栄養指導は栄養指導という観点から統合します。このようなアプローチは、介入群が「同じ介入カテゴリ」と考えられる場合、例えば同じ機能性関与成分の5 mg群と10 mg群を「機能性関与成分」としてまとめたいなどです。また、レビューの焦点が「介入の有無」や「クラス効果」であり、用量やバリエーションの違いに注目しない場合などに適用できます。
\[ \text{Sample size} = N_1 + N_2 = 96 \]
\[ \text{Mean} = \frac{N_1 M_1 + N_2 M_2}{N_1 + N_2} = 35.0 \]
\[ SD = \sqrt{ \frac{ (N_1 – 1)SD_1^2 + (N_2 – 1)SD_2^2 + \frac{N_1 N_2}{N_1 + N_2}(M_1^2 + M_2^2 – 2 M_1 M_2) }{ N_1 + N_2 – 1 } } = 7.8 \]
統合は、スライドに掲載した簡単な数式を使用することで可能です。単純にサンプルサイズが大きくなるので、推定精度があがります。ただし、本当に同一介入と見なせるかの判断が重要です。とくに用量は、用量反応メタアナリシスで用量に依存していないことを確認することが望ましいです。
9.2 アプローチ2: 対照を分割する
2つ目のアプローチは、対照を分割する方法です。ここでは、介入なしを2つに分割します。平均値と標準偏差は据え置きで、サンプルサイズだけ2で除します。
- face‐to‐face VS No intervention
-
Dietary intervention
(face‐to‐face)No intervention Sample size Mean (SD) Sample size Mean (SD) 49 35.2 (7.5) 26 37.1 (7.6)
- online VS No intervention
-
Dietary intervention
(online)No intervention Sample size Mean (SD) Sample size Mean (SD) 47 34.8 (8.2) 26 37.1 (7.6)
これは、介入群をそれぞれ比較して統合したい場合に適しています。介入を独立して解析しやすくなるので、サブグループ解析などしやすくなります。しかし、対照群のサンプルサイズを人工的に半分にするので、推定精度が落ちる欠点があります。
ここまで紹介した介入の統合と対照の分割について、コクランの練習問題
(https://www.cochrane.org/sites/default/files/learning_modules/cesm/tutorials/multi-arm-studies/index.htm) にアクセスして、是非チャレンジしてみてください。9.3 アプローチ3: 特定の比較だけ利用する
3つ目のアプローチは、特定の比較だけ利用する方法です。スライドの例では、対面の栄養指導と対照群だけ抽出して、メタアナリシスに用います。
- face‐to‐face VS No intervention
-
Dietary intervention
(face‐to‐face)No intervention Sample size Mean (SD) Sample size Mean (SD) 49 35.2 (7.5) 52 37.1 (7.6)
- online VS No intervention
- 利用しない
レビューの文脈に合わせやすいので解釈がシンプルになるメリットがあります。しかし、他群を切り捨てたことによるバイアス可能性をレビュー本文で説明する必要があります。
このような方法を駆使して3群以上のデータがある研究をメタアナリシスに利用していきましょう。
異質性を知る
メタアナリシスを行う上で避けて通れないものが異質性です。異質性は、研究間のばらつき全般を指し、「臨床的異質性・方法論的異質性・統計的異質性」に分けられます。
- 臨床的異質性は、参加者の年齢や疾患背景、介入の内容や投与量、測定されるアウトカムが異なることで生じる違いです。
- 方法論的異質性は、研究デザイン、測定方法、解析手法、バイアスのリスクが異なることで生じる違いです。この2つは、定性的に議論され、これらが統計的異質性に反映されます。
- 統計的異質性は、各研究の効果推定値が「偶然のばらつき」では説明できないほど食い違う場合を指しています。
個々の研究結果の信頼区間に重なりが少ない場合、統計的異質性が疑われます。形式的にはカイ二乗検定が用いられ、低いP値や大きなカイ二乗統計量は「偶然以上の差」を示します。ただし、研究数が少ないと検出力が低く、逆に研究数が多いと臨床的に意味のない差も検出してしまうため解釈に注意が必要です。
臨床的・方法論的な多様性は常に存在するため、統計的異質性も不可避と考えられており、「異質性があるか否か」よりも「その影響の大きさ」を評価することが重要です。
10.1 異質性への対応戦略
異質性への対応戦略を紹介します。
| 戦略 | 概要 |
|---|---|
| データの正確性を再確認する | 異質性が著しい場合、抽出・入力ミス(例:SE を SD として入力)や単位解釈誤りが原因であることがあるため、 まずデータの正確性を再確認する。 |
| メタアナリシスを実施しない | 結果の方向が不一致である場合、平均効果を提示すること自体が妥当でない可能性があるため、 定性的レビューに留める判断も正当化される。 |
| 異質性の探索 | サブグループ解析やメタ回帰により原因を探る。 ただし、信頼できるのは事前に定義された解析に限られ、 事後探索は仮説生成にとどめるべきである。 |
| 固定効果モデルによる メタアナリシスを実施する (異質性を無視する) |
固定効果モデルは異質性を考慮しないため、得られる効果推定値は 「存在しない平均的真の効果」を示す危険がある。 信頼区間(CI)は通常より狭くなるため慎重な解釈が必要。 |
| ランダム効果モデルによる メタアナリシスを実施する |
説明不能な異質性に対応する標準的手段。 ただし、探索の代替にはならない。 |
| 効果指標の再考 | 異なる尺度や単位による連続アウトカムでは、平均差よりも標準化平均差の方が適切な場合がある。 また、2 値アウトカムにおいても、リスク比・オッズ比・リスク差の選択によって異質性が変化する。 |
| 研究の除外 | 一部の研究が異質性の原因となっている場合もあるが、結果の不一致理由に明確な根拠がないまま除外すると バイアスを導入する。 感度分析により外れ値を含むか除外するかを検討することが望ましい。 |
異質性への対応戦略としては、データの正確性を再確認やメタアナリシスを実施しないという選択も考えられます。また、異質性の原因の探索、異質性を無視した解析、効果量の変更、研究の除外などがあります。
主解析として推奨されるランダム効果モデルは異質性を数理的に扱う枠組みを提供しますが、異質性が大きい場合には「平均効果」自体が臨床的に意味を持たない可能性があるため、必ず異質性の解釈と探索を伴うべきです。
10.2 ランダム効果モデルに異質性を組み込む
それでは、実施にランダム効果モデルに異質性組み込む流れを確認しましょう。
ランダム効果モデルにおいては、研究間の効果量のばらつきを分散成分として推定し、各研究の重み付けに反映させます。具体的には、研究 i の重みは以下の数式で表現できます。
\[ w_i = \frac{1}{SE_i^2 + \tau^2} \]
この数式にあるSEの二乗は研究
i の効果量推定値の分散であり、タウの二乗は研究間分散です。この数式から分かる通り、固定効果モデルに比べて大規模研究の重みは相対的に小さくなり、研究の異質性を考慮した重み付けとなります。統合推定量は、重み付き平均として以下の数式で表現できます。
\[ \hat{\mu} = \frac{\sum_{i=1}^{k} w_i\, y_i}{\sum_{i=1}^{k} w_i} \]
このようにして、研究内分散と研究間分散の両方を考慮した全体の効果量推定値が得られる。
研究間分散をもとに今後の研究の効果が取りうる範囲を示す指標である予測区間を計算できますが、本稿では省略します。
ここで研究間分散の推定方法を紹介します。様々な方法がありますが、主要な3つがDL、REML、PMです。
- DLは、計算が簡便で実装上も広く普及している一方で、研究数が少ない場合やサンプルサイズの小さい研究を含む場合には、分散を過小推定する傾向が指摘されています。
- REMLは、分散成分を推定するための最尤法の一種で、バイアス修正があります。小規模研究や研究数が少ない場合でも比較的バイアスが少ないです。また、理論的な整合性が高く、統計学的に「推奨される方法」の一つです。
- PMは、モーメント法の一種で、分散成分の推定に「一般化Q統計量」を用います。こちらもDLよりもバイアスが少なく、REMLに匹敵する精度を示すことが多いです。
そのため、メタアナリシスではREMLかPMのいずれかが推奨されます。
10.3 その他の異質性指標
ここまで、研究間分散について説明しましたが、その他の異質性指標を紹介します。
Q統計量は、各研究結果の一貫性を検証するための基本的な検定統計量であり、帰無仮説の下では全ての研究で真の効果が同一であると仮定します。しかし研究数が少ない場合は検出力が不足し、大規模研究ではごく小さな差でも有意になりやすいという限界があります。
この補完的指標として用いられるのがI²であり、総ばらつきのうち異質性に起因する割合を直感的に表現できます。
\[ I^2 = \frac{Q – (k – 1)}{Q} \times 100\% \]
I²の値の目安は以下の通りです。
| I²の値 | 異質性の程度(目安) |
|---|---|
| 0% | 異質性なし |
| 25%前後 | 異質性は小さい |
| 50%前後 | 異質性は中程度 |
| 75%以上 | 異質性が大きい |
直感的にわかりやすいですが、研究数や効果推定の精度に依存するので、過信は禁物です。
要約効果の信頼区間の計算方法を選択する
次は、ランダム効果モデルにおける信頼区間の算出方法について解説します。信頼区間の計算は単なる統計的な手続きに見えますが、実際には結果解釈を大きく左右する重要な部分です。
まず従来から使われてきた Wald (ウォルド) 型信頼区間です。これは標準正規分布を使って、要約効果の信頼区間を求める方法です。計算はシンプルで分かりやすいのですが、研究数が少ない場合に問題が生じます。特に研究数が限られると、区間が過度に狭くなり、不確実性を過小評価してしまいます。
そこで登場するのが Hartung-Knapp-Sidik-Jonkman (ハルトゥング-クナップ-シディック-ヨンクマン) 法、通称HKSJ法です。これは研究間分散の推定の不確実性を区間に反映させる仕組みになっています。具体的には、標準正規分布ではなく自由度のt分布を使うので、信頼区間は広がります。異質性があるときには特に有効で、過度に楽観的な結論を避けられるのがメリットです。ただし注意点もあります。研究数が極端に少ないと逆に区間が広がりすぎる、あるいは研究間分散がゼロのときには狭くなりすぎるというリスクがあります。
まとめると以下の通りです。
| Wald 型 Normal approximation |
HKSJ Hartung–Knapp–Sidik–Jonkman |
|---|---|
|
<分散推定量> \(\hat{V}(\hat{\mu}) = \frac{1}{\sum_{i=1}^k w_i}\) |
<修正分散推定量> \(\hat{V}(\hat{\mu}) = \frac{1}{k-1}\frac{\sum_{i=1}^k w_i^2(\hat{\theta}_i – \hat{\mu})^2}{(\sum_{i=1}^k w_i)^2}\) |
|
<信頼区間> \(\hat{\mu} \pm z_{1-\alpha/2}\sqrt{\hat{V}(\hat{\mu})}\) |
<信頼区間> \(\hat{\mu} \pm t_{k-1,1-\alpha/2}\sqrt{\hat{V}(\hat{\mu})}\) |
|
<特徴>
|
<特徴>
|
基本的には保守的なHKSJを推奨します。とくに研究数が3件以上で、かつ異質性がゼロではない場合にHKSJを推奨するという形になっています。とりあえずHKSJを使うという考えにならないように注意しましょう。
研究数が少ない場合のランダム効果モデルの解釈
ここからは、少数の研究しかない場合にランダム効果メタアナリシスをどう解釈すべきかについて解説します。実はこのケースでは、Wald (ウォルド) 法もHKSJ法も、それぞれに弱点があって完全な解決策は存在しません。そこで、実際のシナリオを3つ取り上げて、どのように解釈すべきかを考えていきます。
| k ≥ 5 | k = 3,4 | k = 2 |
|---|---|---|
|
τ² = 0.0963, I² = 60% 全研究がControl方向 |
τ² = 2.56, I² = 90% 全研究がIntervention方向 |
τ² = 1.40, I² = 75% 2つの研究が別方向 |
|
<HKSJ> HKSJ の方がやや広いCIを与え、不確実性を適切に反映する。 |
<HKSJ> 非常に広いCIを持つ。 |
<HKSJ> t 分布(df=1)の影響を使うため、極端に広い CI になる。 |
|
<Wald> HKSJ よりも CI が狭い。 |
<Wald> 狭い CI で「Intervention側」に収まる。 |
<Wald> CI は狭いが、異質性を無視するので過小評価のリスクがある。 |
Deeks JJ, et al (2024) より引用、改変
最初の例では、研究数が5つ。すべてのオッズ比が『介入は有害』を示しています。異質性はある程度見られ、Tau² (タウスクエアード) やI² (アイスクエアード) もゼロではありません。このとき、HKSJ法を使うと、信頼区間はWald型法よりやや広くなります。これは、研究間の不確実性をきちんと反映しているからです。つまり、研究が2件以上あってTau²がゼロを超えるときは、HKSJ法の方が統計的に望ましいといえます。
次は研究が3つある場合です。ここでは、すべての研究が有益性を示しています。しかし、Tau²とI²はかなり大きく推定されています。HKSJ法を使うと、信頼区間が広がりすぎて、有益性と有害性の両方を含んでしまいます。一方、Wald法は狭い信頼区間で、臨床的に意味のある利益だけを示します。この状況でHKSJ法に頼りすぎると、せっかくの有効な介入を見逃すリスクがあります。したがって、3研究でもWald法を併用し、ただし過小評価の可能性を意識して解釈するのが現実的です。
最後に研究が2つだけのケースです。有益性を示した研究は1つだけです。異質性も大きく見えますが、そもそも2つの研究では推定が不安定です。ここでHKSJ法を使うと、t分布の自由度が1になり、乗数が12.7と極端に大きくなります。結果、信頼区間は過度に広がりすぎる。逆にWald型法を使うと、今度は信頼区間が不自然に狭くなる。つまり、どちらも完璧ではありません。この場合は、Wald型を使うこともあるが、慎重な解釈が必須です。
まとめると、5件以上ならHKSJ法を推奨し、それよりも少ないのであればWald (ウォルド) 法とHKSJ法を併用して得られた結果を慎重に解釈しましょう。
メタアナリシスの実装
13.1 解析データセットの準備
ここまででメタアナリシスをする上で必要の設定がわかったと思います。
それでは、いよいよ実際にメタアナリシスを実装していきましょう。
メタアナリシスができるソフトウェアはたくさんありますが、Rだと簡単に綺麗なフォレストプロットを作成できるので、今回はRでの実装を紹介します。
まず、データセットを用意しましょう。
# dmetarパッケージに含まれる公開データセットをロード
library(dmetar)
data(SuicidePrevention)
# データ構造を確認
str(SuicidePrevention)
データセットは、パッケージのdmetarに含まれるSuicidePreventionを使います。このデータセットは、自殺予防プログラムの効果を検証したランダム化比較試験を題材にしたものです。データセットの中身を確認していきましょう。著者名、発表年に加えて、各介入の症例数、平均値、標準偏差に加えて年齢層と対照群の種類をコード化した変数が含まれるデータセットのようです。
> str(SuicidePrevention)
'data.frame': 9 obs. of 10 variables:
$ author : chr "Berry et al." "DeVries et al." "Fleming et al." "Hunt & Burke" ...
$ n.e : num 90 77 30 64 50 109 60 40 51
$ mean.e : num 14.98 16.21 3.01 19.32 4.54 ...
$ sd.e : num 3.29 5.35 0.87 6.41 2.75 4.63 1.26 0.76 7.24
$ n.c : num 95 69 30 65 50 111 60 40 56
$ mean.c : num 15.54 20.13 3.13 20.22 5.61 ...
$ sd.c : num 4.41 7.43 1.23 7.62 2.66 ...
$ pubyear : num 2006 2019 2006 2011 1997 ...
$ age_group: Factor w/ 2 levels "gen","older": 1 2 1 1 1 1 1 2 2
$ control : Factor w/ 2 levels "no intervention",..: 2 1 1 2 2 1 1 1 1
このデータセットはメタアナリシスに適した形で整備されているので、このまま利用可能です。しかし、今回、みなさまにわかりやすく説明するために少しだけこのデータセットを加工しようと思います。まず、著者と発表年は結合したほうが、わかりやすいので結合しましょう。
つぎに、各群の平均や標準偏差ですが、ここから直接平均差とその標準誤差を計算します。これは、記述統計から直接メタアナリシスをするだけでなく、すでに群間差が計算されているデータセットでメタアナリシスを行うパターンがあることを学んでいただきたいからです。年齢層と対照群の変数はサブグループ解析などに利用できるものですが、今回は使用しないので切り落としていきます。
平均差とその標準誤差の計算はt検定と同義です。必要なデータだけ抽出して、新しいデータセットに作りかえます。
# 前処理
library(dplyr)
df <- SuicidePrevention %>%
mutate(
studlab = paste0(author, " (", pubyear, ")"), # 文献ラベルを生成 (著者+西暦)
MD = mean.e - mean.c, # 群間差 (Mean Difference; MD)
SE = sqrt((sd.e^2 / n.e) + (sd.c^2 / n.c)) # 標準誤差 (独立2群の差の標準誤差)
) %>%
select(studlab, n.e, mean.e, sd.e, n.c, mean.c, sd.c, MD, SE) # 解析に必要な列だけを抽出
# データセットの確認 (上3行)
head(df,3)
> head(df,3)
studlab n.e mean.e sd.e n.c mean.c sd.c MD SE
1 Berry et al. (2006) 90 14.98 3.29 95 15.54 4.41 -0.56 0.5700742
2 DeVries et al. (2019) 77 16.21 5.35 69 20.13 7.43 -3.92 1.0824933
3 Fleming et al. (2006) 30 3.01 0.87 30 3.13 1.23 -0.12 0.2750636
出力してみると上手くできていそうですね。view関数を使用して、データセット全体を確認してみましょう。
# データセットの確認
View(df)
こちらが新たに作り直したデータセットです。
| studlab | n.e | mean.e | sd.e | n.c | mean.c | sd.c | MD | SE |
|---|---|---|---|---|---|---|---|---|
| Berry et al. (2006) | 90 | 14.98 | 3.29 | 95 | 15.54 | 4.41 | -0.56 | 0.570 |
| DeVries et al. (2019) | 77 | 16.21 | 5.35 | 69 | 20.13 | 7.43 | -3.92 | 1.082 |
| Fleming et al. (2006) | 30 | 3.01 | 0.87 | 30 | 3.13 | 1.23 | -0.12 | 0.275 |
| Hunt & Burke (2011) | 64 | 19.32 | 6.41 | 65 | 20.22 | 7.62 | -0.90 | 1.239 |
| McCarthy et al. (1997) | 50 | 4.54 | 2.75 | 50 | 5.61 | 2.66 | -1.07 | 0.541 |
| Meijer et al. (2000) | 109 | 15.11 | 4.63 | 111 | 16.46 | 5.39 | -1.35 | 0.677 |
| Rivera et al. (2013) | 60 | 3.44 | 1.26 | 60 | 3.42 | 1.88 | 0.02 | 0.292 |
| Watkins et al. (2015) | 40 | 7.1 | 0.76 | 40 | 7.38 | 1.41 | -0.28 | 0.253 |
| Zaytsev et al. (2014) | 51 | 23.74 | 7.24 | 56 | 24.91 | 10.65 | -1.17 | 1.747 |
連続変数では記述統計でメタアナリシスをするか、すでに計算された群間差でメタアナリシスをするかのどちらかになります。今回は、2つともデータセットとして整備しましたが、どちらか一方で問題ないです。
群間差の使いどころですが、臨床試験ではベースラインを共変量に投入する場合や、クロスオーバーデザインを採用したりと様々な統計解析手法が採用されており、単純な平均値の比較をしていない場合が数多く存在します。そのようの場合に、例えば共分散分析の群間差をここで採用したりすることができます。
13.2 メタアナリシスのスクリプトを作成する
それでは、実際にメタアナリシスの解析スクリプトを組み立てていきましょう。
今回のパッケージは、metaを使用します。記述統計を使用する場合はmetacont、群間差を使用する場合はmetagenを使用します。ここで、統合方法、モデル、効果量、研究間分散の推定方法、信頼区間の計算方法を設定していきます。
<記述統計を利用する場合>
library(meta)
meta1 <- metacont(
n.e = n.e, mean.e = mean.e, sd.e = sd.e,
n.c = n.c, mean.c = mean.c, sd.c = sd.c,
studlab = studlab,
data = df,
sm = "MD",
common = FALSE,
random = TRUE,
method.tau = "PM",
method.random.ci = "HK",
title = "meta1")
<群間差を利用する場合>
library(meta)
meta2 <- metagen(
TE = MD, seTE = SE,
studlab = studlab,
data = df,
sm = "MD",
common = FALSE,
random = TRUE,
method.tau = "PM",
method.random.ci = "HK",
title = "meta2")
メタアナリシスを実装する際に考えるポイントの例として表に示します。
| 実装するポイント | 統計的選択肢 | Rでの指定方法 |
|---|---|---|
| 統合方法: | 連続変数の平均差を統合するため逆分散法を使用 |
metacont() または metagen()
|
| モデル: | 研究間異質性を考慮するためランダム効果モデルを使用 |
common = FALSE, random = TRUE
|
| 効果量: | 臨床的に直感的な解釈をするために MD を採用 |
sm = "MD"
|
| τ²推定法: | 安定性が高い Paule-Mandel 法を採用 |
method.tau = "PM"
|
| 信頼区間の計算法: | 研究数が 5 以上 20 未満なので Hartung-Knapp 法を採用 |
method.random.ci = "HK"
|
このように1つ1つ設定することができるので、ここで適切なメタアナリシスを構築します。
出力された結果を見ていきましょう。
> meta1
Review: meta1
Number of studies: k = 9
Number of observations: o = 1147 (o.e = 571, o.c = 576)
MD 95%-CI t p-value
Random effects model -0.7426 [-1.5163; 0.0312] -2.21 0.0578
Quantifying heterogeneity (with 95%-CIs):
tau^2 = 0.6014 [0.0044; 4.2610]; tau = 0.7755 [0.0662; 2.0642]
I^2 = 54.9% [4.7%; 78.7%]; H = 1.49 [1.02; 2.17]
Test of heterogeneity:
Q d.f. p-value
17.76 8 0.0231
> meta2
Review: meta2
Number of studies: k = 9
MD 95%-CI t p-value
Random effects model (HK) -0.7426 [-1.5163; 0.0312] -2.21 0.0578
Quantifying heterogeneity (with 95%-CIs):
tau^2 = 0.6014 [0.0044; 4.2610]; tau = 0.7755 [0.0662; 2.0642]
I^2 = 54.9% [4.7%; 78.7%]; H = 1.49 [1.02; 2.17]
Test of heterogeneity:
Q d.f. p-value
17.76 8 0.0231
群間差を利用した場合の結果は、記述統計の結果と一致しました。その他のパラメータも一致しています。これは、群間差がt検定に基づいて計算されているためです。
この群間差の統合は、ANCOVAやクロスオーバーデザインにも適用できるので覚えておきましょう。
次にこれらの結果を利用して、フォレストプロットを作成していきましょう。
13.3 forest plotの作成
今回のメタアナリシスはmetaパッケージを利用しているのでforest関数が使えます。forest関数を使用することで誰でも綺麗なフォレストプロットを作成できます。
3パターンのレイアウトを紹介します。
forest(meta1) # デフォルトのプロット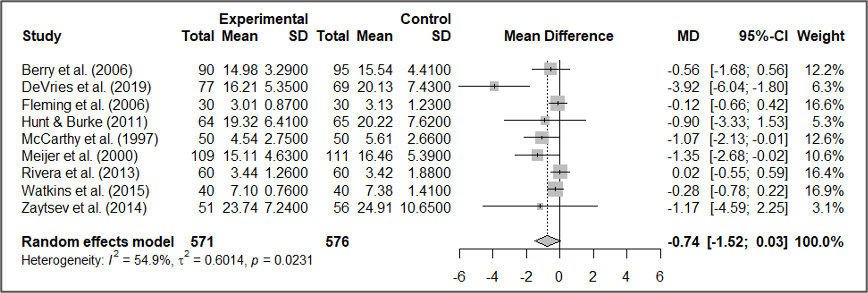
forest(meta1, layout = "RevMan5") # RevMan5風のプロット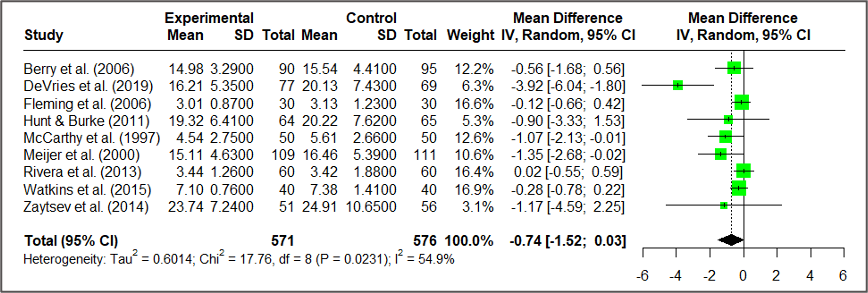
forest(meta1, layout = “JAMA”) # JAMAの論文スタイルを模倣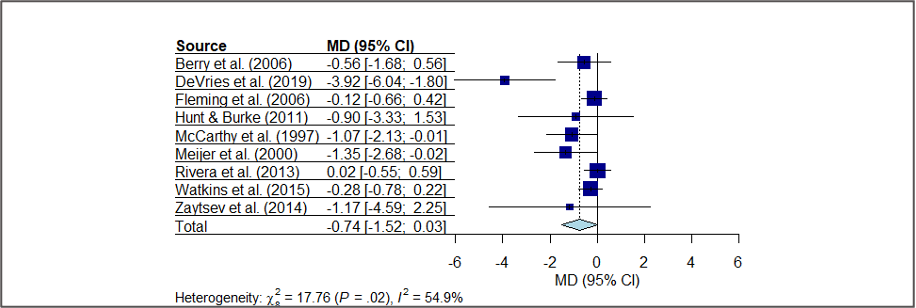
レビューマネージャーやアメリカ医師会雑誌のレイアウトにすることができます。
とくにレビューマネージャーのスタイルはコクランが推奨するレイアウトなので必要な情報がすべて含まれているだけでなく、読者や査読者にとっても見慣れたスタイルであるためわかりやすいです。
また、これらのレイアウト以外にもフォレストプロットを美しくする方法はあります。
forest(meta1,
layout = "RevMan5",
# 色の設定
col.diamond = "black", # 総合効果のダイヤモンドの色
col.square = "#1c98ac", # 各研究の四角の色
col.square.lines = "#1c98ac", # 四角のラインの色
col.label.right = "red", # 右側ラベルの色
col.label.left = "#1c98ac", # 左側ラベルの色
# ラベル設定
label.right = "Favours Control", #対照群が有利
label.left = "Favours Experimental“) #実験群が有利
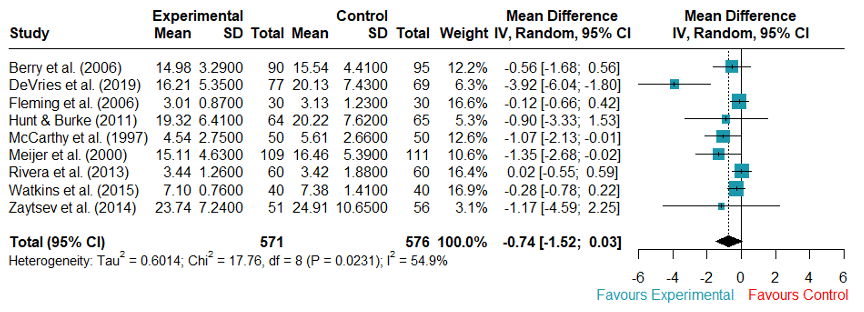
Metaパッケージのマニュアルにアクセスして、forest関数でできることに確認できます。
(https://cran.r-project.org/web/packages/meta/meta.pdf)
機能性表示食品のための書き方
#28. より良い方法の書き方
最後に使用したメタアナリシスの手法の報告方法を紹介します。
届け出の様式 (別紙様式 (Ⅴ)-15) でよくある記入例をスライドに示しました。
この様式でメタアナリシスの方法を記載する箇所は、3つあります。
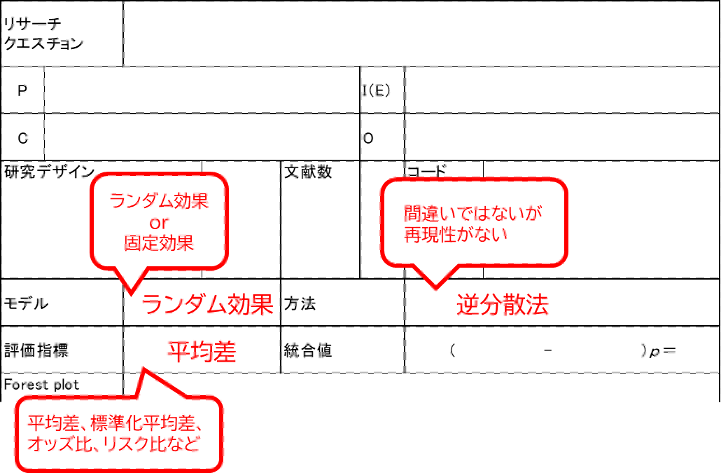
モデルの項では、ランダム効果モデルなのか固定効果モデルなのかを記載します。ここは、問題なく記載できていると思います。
評価指標も平均差やオッズ比などを記載するので、問題はないのですが、一部MDとSMDを混同してしまっている例が見受けられました。例えば、ここでMDと記載しているのにフォレストプロットもみるとSMDになっている例があります。MDとSMDは、本講演でもお話させていただいたように標準偏差の取り扱い方において解釈が異なります。そのため、ここは慎重に記載しましょう。
次の方法の項に問題があると考えています。ここで、逆分散法と記載している場合が多いですが、これだけの記載だと第三者が資料を見て再解析としてメタアナリシスをした場合に同じ結果を得られない場合があります。つまり、再現性がない状態です。この様式内もしくは本文中に、研究間分散の推定方法と信頼区間の推定方法を記載して、再現性のある結果であることを主張していきましょう。
まとめ
まず、適切な統合方法を選択することが重要です。メタアナリシスは「複数研究の知見を統合して平均効果を推定」する手法であり、固定効果モデルやランダム効果モデルを利用します。統合結果は「母集団の唯一の真値」ではなく「状況を平均化した効果」と理解しましょう。
次に、効果量と異質性の理解が不可欠ということです。効果量は、平均差や標準化平均差など様々なものがありますが、SRの文脈に合わせて選択しましょう。異質性は適切な指標を利用して評価することがメタアナリシスの信頼性を左右することにつながります。
最後に信頼区間の解釈に注意することが重要です。Wald法の限界を知り、HKSJ法も活用して、過大評価のリスクの対策をしましょう。
本稿は、メタアナリシスの基礎的な部分のみの説明となってしましましたが、予測区間の算出方法やメタ回帰分析、用量反応メタアナリシスなどメタアナリシスの抑えるべきポイントはまだまだあります。もし、これらの手法について気になることがあれば弊社までお問い合わせください。

参考文献
- Deeks JJ, Higgins JPT, Altman DG, McKenzie JE, Veroniki AA (editors). Chapter 10: Chapter 10: Analysing data and undertaking meta-analyses [last updated November 2024]. In: Higgins JPT, Thomas J, Chandler J, Cumpston M, Li T, Page MJ, Welch VA (editors). Cochrane Handbook for Systematic Reviews of Interventions version 6.5. Cochrane, 2024. Available from cochrane.org/handbook.
- Higgins JPT, Li T, Deeks JJ (editors). Chapter 6: Choosing effect measures and computing estimates of effect [last updated August 2023]. In: Higgins JPT, Thomas J, Chandler J, Cumpston M, Li T, Page MJ, Welch VA (editors). Cochrane Handbook for Systematic Reviews of Interventions version 6.5. Cochrane, 2024. Available from cochrane.org/handbook.
- Higgins JPT, Eldridge S, Li T. Chapter 23: Including variants on randomized trials [last updated October 2019]. In: Higgins JPT, Thomas J, Chandler J, Cumpston M, Li T, Page MJ, Welch VA (editors). Cochrane Handbook for Systematic Reviews of Interventions version 6.5. Cochrane, 2024. Available from cochrane.org/handbook.
- Murad MH, Wang Z, Chu H, Lin L. When continuous outcomes are measured using different scales: guide for meta-analysis and interpretation. BMJ. 2019 Jan 22;364:k4817. doi: 10.1136/bmj.k4817. PMID: 30670455; PMCID: PMC6890471.
- Axon E, Dwan K, Richardson R. Multiarm studies and how to handle them in a meta-analysis: A tutorial. Cochrane Evid Synth Methods. 2023 Dec 20;1(10):e12033. doi: 10.1002/cesm.12033. PMID: 40476010; PMCID: PMC11795958.
- Langan D, Higgins JPT, Simmonds M. Comparative performance of heterogeneity variance estimators in meta-analysis: a review of simulation studies. Res Synth Methods. 2017 Jun;8(2):181-198. doi: 10.1002/jrsm.1198. Epub 2016 Apr 6. PMID: 27060925.
- Balduzzi S, Rücker G, Schwarzer G. How to perform a meta-analysis with R: a practical tutorial. Evid Based Ment Health. 2019 Nov;22(4):153-160. doi: 10.1136/ebmental-2019-300117. Epub 2019 Sep 28. PMID: 31563865; PMCID: PMC10231495.